eine Frage, ob mein Ansatz korrekt ist
Die Aufgabe:
eine Schachtel soll ein Volumen von 80cm³ erhalten. Die Schachtel soll außerdem doppelt solang wie breit sein. Die Breite der Klebefalze entspricht der Hälfte bzw. einem Viertel der Schachtelbreite. Welche Maße muss die Schachtel haben, wenn minimal Material verwendet werden soll.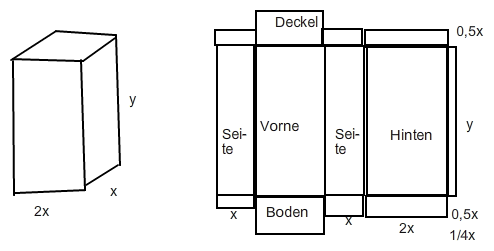
Mein Ansatz:
HB: A=[2*(2x*y) + 2*(x*y) + 2*(2x*x) + 4*(x*0,5x) + 2*(2x*0,5x) + (1/4x*y)]
Vorne+Hinten 2 Seiten Deckel+Boden 4 Klebefalzen Seite 2 Klebefalzen "Hinten" seitliche Klebefalz "Hinten"
NB :80cm³=2x²*y
Stimmt das so weit? Nun eben weiter vorfahren, wie gewohnt
Gruß
Luis