Mithilfe eines Punktes und einer Fläche eine Geradengleichung ermitteln

Question

ich sitze jetzt schon längere Zeit vor dieser Aufgabe, komme aber auf kein richtiges Ergebnis, hoffe mir kann jemand helfen.

Es ist gegeben:

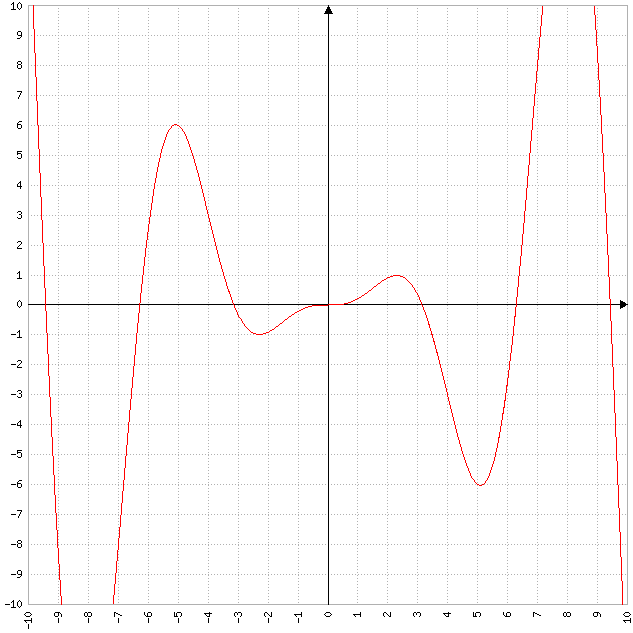
f(x)=1/4*x^2*sin(x) mit x∈]-2π;2π[

f(x)=K_f

Aufgabenstellung:

Das Schaubild K_f und die x-Achse schließen im 1. Quadranten eine Fläche ein. Eine Gerade durch den Punkt N(π|0) halbiert diese bestimmte Fläche. Bestimmen Sie die Gleichung dieser Geraden.

Zuerst habe ich die Fläche im Intervall [0;π] ausgerechnet, also:

F(x)=-((x^2-2)*cos(x)-2*x*sin(x))/(4)

A_ges=F(π)-F(0) = (π^2-4)/(4) ≈1,47

Jetzt weiß ich nur nicht, wie ich weitermachen soll, ich habe schon versucht den Hochpunkt der Funktion f(x)/(2) im Intervall [0;π] zu ermitteln, da ja die Fläche die hälfte sein soll, habe ich die Funktion durch zwei geteilt.

Durch den Hochpunkt habe ich mir halt gedacht, das ich jetzt wissen müsste, das die Gerade durch diesen y-Wert des Hochpunktes durch die Funktion f(x) gehen muss, aber ist vermutlich Schwachsinn.

Zum Schluss kam ich dann auf y=-0,57*x+1,79

Aber dieses Ergebnis ist falsch, da wenn ich eine Differenzfunktion bilde, also h(x)=f(x)-y komme ich nicht auf die hälfte der Fläche, die es ja sein soll.

Hoffe mir kann jemand helfen :)

Comments

Ich  habe die Aufgabe gelöst, ich schreibe die Lösung auch gleich mal dazu, für die, die sich dafür interessieren :)

Die Funktion schneidet die x-Achse, daher gilt:

f(x)=0

x₁=0 ; x₂=π

Geradengleichung:

g(x)=mx+b

g(π)=0 = m*π+b=0 => b=-m*π

daraus folgt:

g(x)=m*x-m*π

Schnittpunkt ermitteln:

f(x)=g(x)

=> m=(x^2*sin(x))/(4*(x-π))

-------------------------------------------

I=[0;π]

∫f(x)dx=(π^2-4)/4

Gleichungssystem:

∫(Links) [x;π]                ∫(Rechts) [0;π]

∫f(x)-g(x)dx=∫f(x)dx

wobei m=(x^2*sin(x))/(4*(x-π))

=> x=1,5318

In m einsetzen ergibt dann m=-0,364

Geradengleichung:

g(x)=-0,364*x+1,144

Answer 1

f(x) = 1/4·x^2·SIN(x)

F(x) = (2·x·SIN(x) - (x^2 - 2)·COS(x))/4

∫ (0 bis pi) f(x) dx = (pi^2 - 4)/4

∫ (0 bis k) f(x) dx + 1/2·(pi - k)·f(k) = (pi^2 - 4)/8

((2 - k^2)·COS(k) + 2·k·SIN(k) - 2)/4 + 1/2·(pi - k)·(1/4·k^2·SIN(k)) = (pi^2 - 4)/8

Ich komme über eine Numerische Lösung auf

k = 1.531760843

Vielleicht findet aber noch jemand eine Möglichkeit eine algebraische Lösung zu finden.

Jetzt braucht nur noch die Gerade durch die Punkte (pi | 0) und (1.532 | f(1.532)) ermittelt werden.

Comments

Danke für die Antwort :)Gute Idee noch eine Dreiecksfläche mit einzubauen.
Aber diese Lösung kann man nur in diesem Speziellen Fall verwenden und meine im allgemeinen, oder irre ich mich da?Aber deine ist Eleganter :D