volumen einer quadratischen pyramide

Question

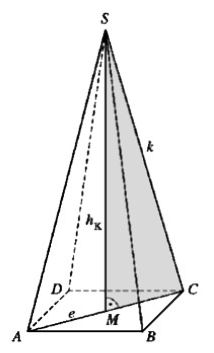
Berechne das Volumen einer quadratischen Pyramide mit der Grundkante $a$, der Höhe $h_{\mathrm{K}}$, der Seitenkante $k$ und der Diagonale $e$ der Grundfläche.

a) $a=5,2 \mathrm{~cm}, \quad k=9 \mathrm{~cm}$

b) $a=7,5 \mathrm{~cm}, \quad k=12,4 \mathrm{~cm}$

c) $e=6 \mathrm{~cm}, \quad k=10,6 \mathrm{~cm}$

d) $e=8,15 \mathrm{~m}, \quad k=15 \mathrm{~cm}$

e) $h_{\mathrm{K}}=8,2 \mathrm{cm}, \quad k=9,7 \mathrm{~cm}$

f) $h_{\mathrm{K}}=4,7 \mathrm{~cm}, \quad k=7,6 \mathrm{~cm}$

Comments

Benutze zur Lösung einfach das Programm in der Formelsammlung: Pyramide online berechnen

Answer 1

Es gilt

(a/2)² + (a/2)² + h² = k²

h = √(k² - a²/2)

und auch 

a² + a² = e²

a = √2/2·e

Answer 2

a)

zuerst berechnen wir hk mit Pyth.4

hk = √ k² -(a/2)²

hk = √ 81 cm²  - (2,6)²

hk = √74,24 = 8,6 cm !

Nun V !

V =1/3 G  *  h  =  27,04  *  8,6 = 77,5 cm³ !!