Aufgabe:
Die Punkte \( P_{0}, P_{1} \) und \( P_{2} \) definieren ein Dreieck in der Ebene:
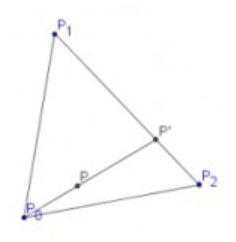
Jeder Punkt \( P \) innerhalb des Dreiecks kann beschrieben werden durch
\( P=u P_{0}+v P_{1}+w P_{2}, \quad \text { mit } u+v+w=1 \text { und } u, v, w \geq 0 \)
\( u, v, w \) sind also die baryzentrischen Koordinaten von \( P \).
a) Man stelle \( P \) dar als Punkt auf der Geraden zwischen \( P_{0} \) und \( P^{\prime} \), wobei \( P^{\prime} \) ein Punkt auf der Geraden zwischen \( P_{1} \) und \( P_{2} \) ist. Es ergibt sich eine Gleichung für \( P \) mit 2 Parametern, z.B. \( s, t \).
b) Man drücke \( u, v, w \) in Termen von \( s \) und \( t \) aus.
Ansatz/Problem:
Wie genau Forme ich also eine Geradengleichung auf einen Punkt um? In diesem Falle sind es ja 2 Geraden?
Meine Überlegung war folgende: P = P0 + s*P' + t*(P1-P2)
Geht dies in die richtige Richtung?