a) Berechne Breit und Höhe von Bildschirmen mit den Bilddiagonalen 69cm und 89cm bei einem 4:3-Format. Um wie viel cm² unterscheiden sich die beiden Bildschirmflächen?
Wir haben jeweils 4 unbekannte Längen als Breite des Bildschirms und 3 unbekannte Längen als seine Höhe (wegen des 4:3-Formats):
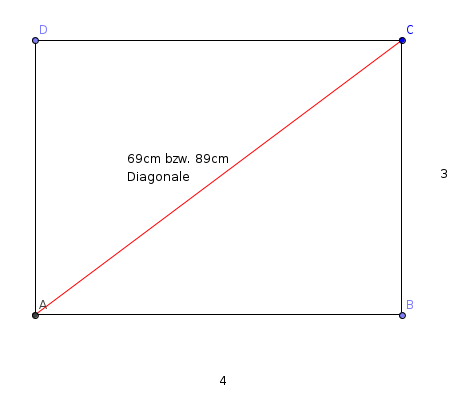
Nun können wir einfach einsetzen:
692 = (4x)2 + (3x)2
4761 = 16x2 + 9x2 = 25x2 | : 25
190,44 = x2 | Wurzel
x = 13,8
Der Bildschirm ist also 4 * 13,8cm = 55,2cm breit und 3 * 13,8cm = 41,4cm hoch.
Bildschirmfläche = 55,2cm * 41,4cm = 2285,28cm2
892 = 25x2 | : 25 und Wurzel
x = Wurzel aus 316,84
Breite: 4 * 17,8cm = 71,2cm; Höhe: 3 * 17,8cm = 53,4cm.
Bildschirmfläche = 71,2cm * 53,4cm = 3802,08cm2
Die beiden Bildschirmflächen unterscheiden sich um 3802,08cm2 - 2285,28cm2 = 1516,8cm2
Besten Gruß