Bestimme von folgenden Funktionen die Nullstellen... f: y = 1/4x^2 + 5/2x - 9/4

Question

Bestimme von folgenden Funktionen die Nullstellen, Fixpunkte, Extremwerte und die Tangente in den Nullstellen. Berechne anschließend in welchem Punkt die Funktion  die angegebene Steigung k besitzt und zeichne den Graphen im angegebenen Intervall.

f: y = 1/4x² + 5/2x - 9/4

k = -3/2

[0,11]

 

Ich bedanke mich im Voraus

Answer 1

Hi,

f: y = 1/4x² + 5/2x - 9/4

 

Nullstellen:

f=0

1/4x² + 5/2x - 9/4=0   |*4

x^2+10x-9=0

pq-Formel

x₁=-5-√34 und x₂=-5+√34

 

Fixpunkte:

f(x)=x

1/4x² + 5/2x - 9/4=x      |-x

1/4x² + 3/2x - 9/4=0      |*4

x^2+6x-9=0

x₃=-3-3√2  und x₄=-3+3√2

Da Fixpunkt x-Wert=y-Wert:

S₃(-3-3√2|-3-3√2)   und S₄(-3+3√2|-3+3√2)

 

Extremwerte:

f'(x)=x/2+5/2=0

x₅=-5

Damit in f''(x) -> herausfinden ob und um welches Extremum es sich handelt.

f''(x)=5/2

f''(-5)>0 -> Minimum

Damit in f(x):

f(-5)=-8,5

Tiefpunkt bei T(-5|-8,5)

 

Tangente in den Nullstellen:

-> Vorgehen: Steigung bestimmen, indem man die Nullpunkte in die erste Ableitung gibt. Dann den Nullpunkt in die Geradengleichung der Form y=mx+b eingeben. Damit lässt sich das nun noch Unbekannte b bestimmen.

x₁=-5-√34 und x₂=-5+√34

f'(x₁)=-√(17/2)

f'(x₂)=√(17/2)

 

y₁=-√(17/2)*x-17-5√(17/2)

y₂=√(17/2)*x-17+5√(17/2)

 

Steigung k=-3/2:

f'(x)=-3/2

f'(x)=x/2+5/2=-3/2   |-5/2

x/2=-4                       |*2

x=-8

 

Damit in f(x):

y=-6,25

Die Steigung k findet man im Punkt K(-8|-6,25).

 

Schaubild:

 

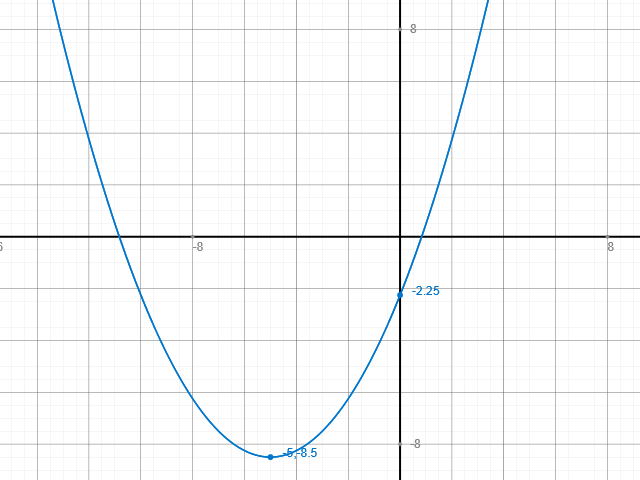
Grüße

Comments

Sicher, dass in der Aufgabe nicht plus und minus vertauscht sind?

---

Würde Sinn bzgl dem zu zeichnenden Intervall ergeben.

 

Das von mir vorgestellte Prinzip ist aber das gleiche und sollte leicht übertragen werden können, sowie die vorgestellten Werte (die hoffentlich richtig sind).

---

Ich bedanke mich für die schnelle Antwort. Ich habs verstanden.