Zeigen Sie für z, w∈ℂ: 2|z|^2 + 2|w|^2 = |z+w|^2 + |z-w|^2 und deuten Sie die Formel mit Parallelogramm

Question

Zeigen Sie für z, w ∈ ℂ:

\( |z+w|^{2}+|z-w|^{2}=2\left(|z|^{2}+|w|^{2}\right) \)

Deuten Sie die Formel geometrisch anhand eines passenden Parallelogramms.

Answer 1

z = a + bi
w = c + di

|z + w|^2 + |z - w|^2
= |a + bi + c + di|^2 + |a + bi - c - di|^2
= (a + c)^2 + (b + d)^2 + (a - c)^2 + (b - d)^2
= 2·a^2 + 2·b^2 + 2·c^2 + 2·d^2
= 2 * (a^2 + b^2 + c^2 + d^2)
= 2 * (|a + bi|^2 + |c + di|^2)
= 2 * (|z|^2 + |w|^2)

Schaffst du das mit dem Parallelogramm selber ?

Comments

Leider habe ich keine Ahnung wie das mit dem Parallerlogramm gehen soll.

Wie kommt man von der drittletzten auf die vorletzte Zeile?

---

das ist doch das gleiche wie eine vektoraddition mit 2|z|²+2|w|² oder?! ich mein das ist doch nen parallelogramm... kann auch sein das ich mich irre aber eine antwort wäre nett :D

---

Wir können doch wie folgt schreiben

|a + bi| = √(a^2 + b^2)

also

|a + bi|^2 = √(a^2 + b^2)^2 = a^2 + b^2

---

aber wie kommt man von Ι a+bi Ι auf ∫(a^2 + b^2 )

---

Das ist nach dem Pythagoras die Vektorlänge. So ist der Betrag einer komplexen Zahl definiert.

---

okay danke..das klingt logisch..

allerdings verstehe ich dann nicht wie ich Ι ΙzΙ - ΙwΙ Ι ≤ Ιz-wΙ zeigen soll..kannst du mir das vielleicht erklären? in der Vorlesung die sich um dieses Thema drehte war ich leider nicht da, weil ich eine andere Vorlesung besuchen sollte..nun sitze ich schon seit einer Stunde hier und komme nicht weiter..die ähnliche Aufgabe oben hilft mir auch nur geringfügig..und ich benötige dies für einen längeren Beweis

LG

---

Die Frage ist mit anderen Unbekannten gerade von mir beantwortet worden.

https://www.mathelounge.de/66672

---

ja aber doch für ein anderes Beispiel. du hast dies ja da nur am ersten Beispiel vorgeführt kanns du dies auch nochmal explizit für das 2. machen? also für:
||z| − |w|| ≤ |z − w|

---

Das würde in etwa wie folgt aussehen:

https://docs.google.com/document/d/1EwvDcx04q1RIhTJtCDapGwUJUPfA13LE_64jRPx4U0Q/pub

---

okay danke
nur eine Frage:

wie kommst du auf den linken der Term der 5. Zeile. Der rechte ist klar..da wurden die Klammern ausmultipliziert..aber wie entsteht der linke Term? woher kommt die -2 und wie kann aus einem minus ein mal werden?

---

Schon mal etwas von den binomischen Formeln gehört

(a - b)^2 = a^2 - 2ab + b^2

Ich habe hier nur die -2*.. nach vorne genommen, weil das der kompliziertere Ausdruck ist.

Answer 2

@Anonym. Hier eine Skizze in der komplexen Zahlenebene zum Zusammenhang mit einem Parallelogramm.

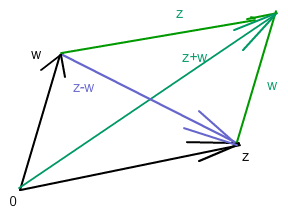
Cosinussatz auf Parallelogrammhälften anwenden:

Teildreieck links oben: |z|^2 + |w|^2 = |z+w|^2 - 2|z||w| cos (Winkel links oben)

Teildreieck links unten: |z|^2 + |w|^2 = |z-w|^2 - 2|z||w| cos (Winkel links unten)

----------------------------------------------------------------------------------------Summe

                                      2|z|^2 + 2|w|^2 = |z+w|^2 + |z-w|^2    qed

Begründung cos-Anteil fällt weg.

Denn cos(Winkel links oben) = - cos(Winkel links unten),

da (Winkel links unten) = 180° - (Winkel links oben)

 

Comments

Danke war sehr hilfereich denke nun hab ich es verstanden :)