Rotationsparaboloid (Mantelfläche z=1/2 r^2 ) bis zur Höhe h=3 Wasser füllen. Arbeit? (Mehrfachintegral)

Question

Der skizzierte Behälter (Rotationsparaboloid mit der Mantelfläche z=1/2 r² ) soll bis zur Höhe h=3 mit Wasser gefüllt werden. Welche Arbeit ist dabei mindestens aufzuwenden?

Hinweis: Die hier aufzubringende Hubarbeit entspricht der potentiellen Energie! (E_pot = W_Hub =mgz)

 

Kann mir hier mal Jemand helfen, ich habe keine Ahnung wie ich da anfangen soll!!!

Comments

Auf welcher Höhe befindet sich das Wasser, bevor es gehoben wird?

---

Ganz unten, also auf Null würde ich sagen!

---

Bis wann brauchst Du denn eine Antwort?

---

Nächste Woche würde reichen!

---

Kommentar siehe unten!

Answer 1

Hier mal das was ich herausgefunden habe:

Bild 1: Zylinderkoordinaten, Integrationsgrenzen, Volumenintegral, Schwerpunktberechnung Teil 1

 

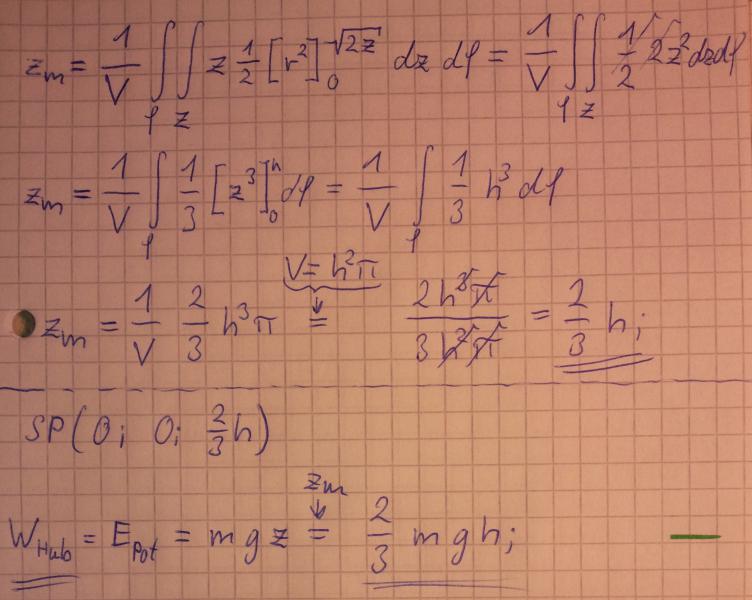
Bild 2: Schwerpunktberechnung Teil 2, Hubarbeit

 

Wenn man davon ausgeht, dass das gesamte Wasser auf Null-Niveau ist und von dort in den Rotationskörper gepumpt wird, dann braucht man lediglich die z-Koordinate des Schwerpunkts und kennt so die Höhendifferenz und damit die potentielle Energie, die im Wasser steckt bzw. die Arbeit, die man aufwenden muss, um das Wasser dort hin zu bringen.

Bitte prüfe alles sorgfältig. Ich kann Dir nicht garantieren, dass alles richtig ist. Vielleicht gibt es auch eine einfachere Vorgehensweise. Wäre gut wenn jemand anderes hier im Forum mein Ergebnis kommentieren könnte.

Wenn Du eine Lösung hast, dann poste sie bitte hier.

 

lg JR

Comments

Danke erst mal, ich habe jetzt auch die richtigen Lösungen, stimmen leider nicht mit Deiner überein.

Grenzen:

Phi: 0 - 2Pi

r: 0 - Wurzel 6

z: 1/2 r²  -  3

Wassermasse m = 9 * Pi * Rho

Schwerpunktshöhe z_s= 2

Arbeit W = 18 * Pi *  Rho * g

---

Wie kommt man denn bei r: auf das "wurzel 6" oder wie du es geschrieben hast "wurzel 2*z"

---

Also wenn ich das richtig sehe habe ich sehr wohl richtig gerechnet. Ich habe lediglich nicht vollständig eingesetzt.

Mein Ergebnis für: V = h^2*pi.
Mit h=3 --> V = 9*pi. Wenn Du die Masse brauchst. M = rho*V = 9*pi*rho. Entspricht Deinem Ergebnis!

Mein Ergebnis für den Schwerpunkt: z_s=2/3*h.
Mit h=3 -->z_s=2. Entspricht Deinem Ergebnis!

Mein Ergebnis für Whub = 2/3*m*g*h.
Mit h=3 und m=V*rho=9*pi*rho --> 18*pi*rho*g. Entspricht genau Deinem Ergebnis!

Das einzige, das bei mir anders ist, das sind die Grenzen, aber da ist man nicht unbedingt festgelegt.
 

Für z gilt: 0 ≤ z ≤ h außerdem gilt der Zusammenhang z = 1/2*r^2. Über diesen Zusammenhang setzt der Maximalwert für z (das ist hier das h) die Grenze für r. z=h=1/2*r^2 --> r = sqrt(2*h). Es wird nur der Positive Ast der Parabel betrachtet (es wird ja nur ein Parabelast rotiert und nicht beide), damit entfällt die negative Lösung. Mit h=3 --> r=sqrt(6).

Und Danke, dass Du die Lösung postest. Das machen nur wenige, ist aber immer gut zur Kontrolle.

 

lg JR

---

Danke, aber ich verstehe nicht wie ich auf die Grenzen komme, kannst Du mir das noch mal genau erklären? Ich habe da so dermaßen Schwierigkeiten mit!!!

---

Bitte stell nochmal eine Frage im Forum (z.B.: "Wie erstelle ich die Grenzen für ein Mehrfachintegral?", mit einem Verweis auf dieses Beispiel). Vielleicht haben die Anderen einen besseren Erklärungsansatz.

Ich komm im Moment nicht dazu das gut zu erklären.