komplexe Zahl z= -1+i in Polarkoordinaten darstellen

Question

was ist die Polardarstellung von z=-1+i?

Answer 1

                    

Answer 2

Allgemein ist die Polardarstellung einer imaginären Zahl $z=r(\cos \varphi + i \cdot \sin{\varphi})=re^{i \varphi}$. Wenn $z=a+i\cdot b$ dann ist $r=\sqrt{a^2+b^2}$ und $\varphi = \arctan (b/a)$. Hier ist $z=-1+i$

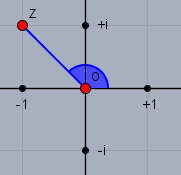
Also $r=\sqrt{1^2+1^2}=\sqrt{2}$ und $\varphi=\arctan{(-1/1)}=3\pi/4$ - Folglich

$$z=\sqrt{2}\cdot(\cos{\frac{3\pi}{4}} + i \cdot \sin{\frac{3\pi}{4}} )=\sqrt{2}\cdot( \frac{-1}{2}\sqrt{2} + i \cdot \frac{1}{2}\sqrt{2} )=\sqrt{2} \cdot e^{i\frac{3\pi}{4}}$$ siehe auch Polarform.

Gruß Werner

Comments

Wäre es nicht der arctan von -1?

---

Wäre es nicht der arctan von -1?

Und stimmt diese Formel nicht?

---

Doch - ich hatte zunächst das Minuszeichen übersehen, habe das aber dann korrigiert (s.o.).

---

ist dann die Formel, die ich habe, falsch?

---

nein - die Formel ist richtig. Ist doch die gleiche, die ich in meiner Antwort geschrieben habe.