Zeige die Identität: Summenzeichen ..... = 1 - qn. lim n-> unendlich n-nq+1-q = 1-q... richtig?

Question

Ist lim n-> unendlich n-nq+1-q = 1-q... richtig?

hab das folgende Problem:

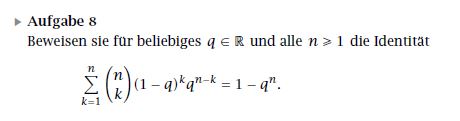
mit  der vollständigen Induktion folgt...

.

.

.

↔ $$1-{ q }^{ n }+(n-nq+1-q)\cdot { q }^{ n }=1-{ q }^{ n }\cdot { q }^{ 1 }$$

↔ $$\lim _{ n\rightarrow \infty} 1-1+n-nq+1-q=1-1\cdot { q }$$

da n -> ∞ sind die ns alle 0 und dann folgt

↔ 1 - q = 1 - q

↔ 1= 1 also ist der beweis fertig?

Comments

mir fällt grad auf, das mit n = 0 ist quatsch.. habt ihr eine idee wie das gehen soll?

---

Tipp: Binomischer Lehrsatz

---

achso also nicht mit induktion!? dachte es geht vielleicht auch mit aber bekomm halt die "n - nq" nicht weg am ende ...

$$\lim _{ n\rightarrow \infty } n-nq+1-q=1- { q }$$

wie geht das denn mit der binomischen formel genau?

(1-q)^k ähnelt schon der binomischen formel aber doch nur bei k = 2 ?!   

---

Ich weiß ja nicht was du mit dem Limes hier willst. Es ist obige Formel zu zeigen. Wenn ihr den binomischen Lehrsatz schon bewiesen habt ist die Aufgabe eigentlich schon gelöst:

$$1=1^n=(1-q+q)^n=\sum_{k=0}^{n}{\begin{pmatrix} n\\k \end{pmatrix}(1-q)^kq^{n-k}}=q^n+\sum_{k=1}^{n}{\begin{pmatrix} n\\k \end{pmatrix}(1-q)^kq^{n-k}}$$

---

"  (1-q)^k ähnelt schon der binomischen formel aber doch nur bei k = 2 ?!   _"

Binomischer Lehrsatz: https://de.wikipedia.org/wiki/Binomischer_Lehrsatz#Binomischer_Lehrs…

Answer 1

$$1=1^n=(1-q+q)^n=\sum_{k=0}^{n}{\begin{pmatrix} n\\k \end{pmatrix}(1-q)^kq^{n-k}}=q^n+\sum_{k=1}^{n}{\begin{pmatrix} n\\k \end{pmatrix}(1-q)^kq^{n-k}}$$

Comments

die einzelnen schritte kann ich einfach nicht nachvollziehen... wieso ist 1ⁿ = (1-q+q)ⁿ und wieso ist das = ∑ⁿ_k=0 (ⁿ_k) (1-q)^k q^n-k ? das sieht doch alles nicht ähnlich aus?

wird vielleciht zu viel arbeit aber kannst du eventuell die einzelnen schritte auf ein blatt papier aufschreiben und hochladen?

---

wieso ist 1ⁿ=(1-q+q)ⁿ?

weil -q+q=0 und 1+0=1

Das ist einfaches plusrechnen ;)

wieso ist das ∑ .... ?

Das ist der binomische Lehrsatz, angewendet mit a=(1-q) und b=q, den Lu dir oben verlinkt hat. falls du einen Beweis für den brauchst schau z.B hier nach:

https://de.wikibooks.org/wiki/Beweisarchiv:_Algebra:_Ringe:_Binomisc…

---

haha gar nicht gesehen... ok danke dir jetzt machts sinn...

Answer 2

> $\lim _{ n\rightarrow \infty} 1-1+n-nq+1-q=1-1\cdot { q }$

Das stimmt nicht. Für zum Beispiel q = 2 ist 1-1+n-nq+1-q = -n-2, divergiert also für n→∞, aber 1-1·q = -1.

Der Beweis ist also nicht fertig.