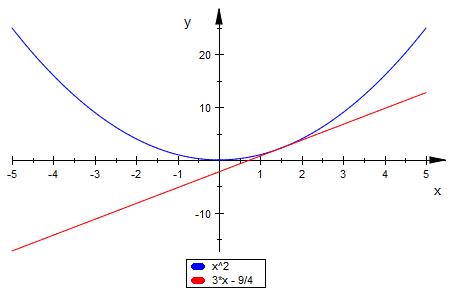
Ich nehme einmal als Normalparabel
f ( x ) = x^2 an.
f ´( x ) = 2 * x
Für den Berührpunkt einer Tangente
t ( x ) = a * x + b
t ´( x ) = a
gilt
f ( x ) = t ( x ) | gleiche Koordinaten
f ´ ( x ) = t ´ ( x ) | gleiche Steigung
a = 3
2 * x = 3
x = 3 / 2
Koordinaten ermitteln
f ( x ) = ( 3/2 )^2 = 9 / 4
B ( 3/2 | 9/4 )
In t einsetzen
t ( x ) = 3 * x + b
t ( 3/2 ) = 3 * 3/2 + b = 9/4
b = 9/4 -9/2
b = - 9 / 4
t ( x ) = 3 * x - 9/4