hey!
Sitze gerade an einer Aufgabe zu Populationsentwicklungen (Tierpopulation) und komme bei der letzten Teilaufgabe nicht weiter!
Aufgabe:
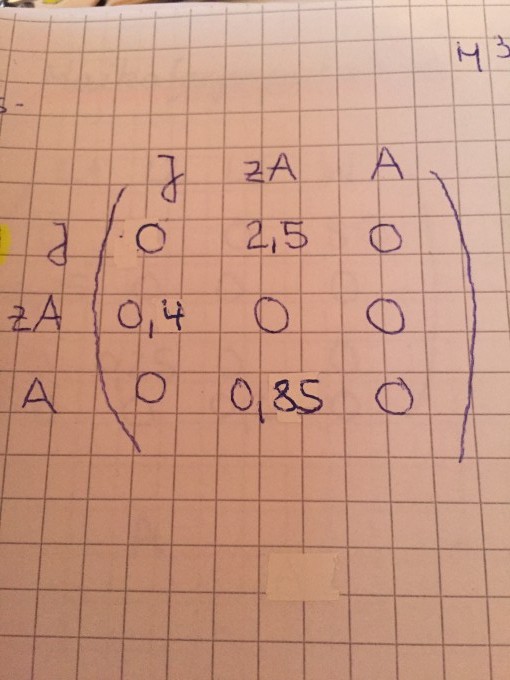
Bei einer Tierpopulation geht man davon aus, dass innerhalb einer Periode nur 40% der Jungtiere das zeugungsfähige Alter erreichen. Von den Tieren des zeugungsfähigen Alters sterben etwa 15% in einer Periode. Die Alttiere einer Periode sterben sämtlich bis zum Ende der Periode. Außerdem rechnet man innerhalb einer Periode mit einer Reproduktionsrate von durchschnittlich 2,5 Jungtieren pro Tier im zeugungsfähigen Alter. (Matrix - Anhang 1)
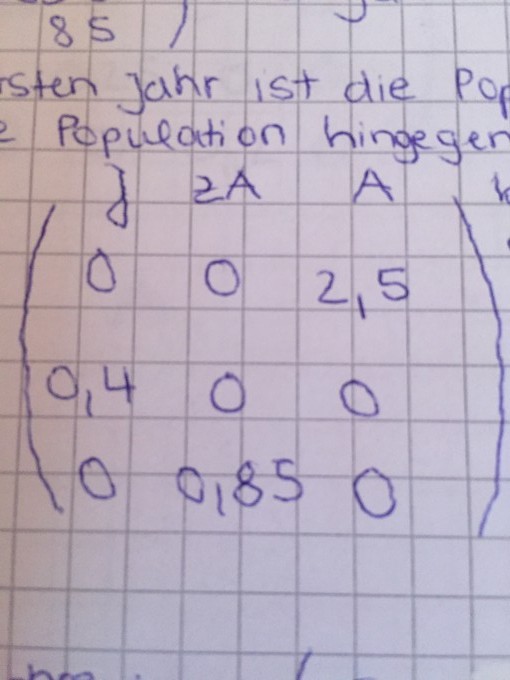
Jedoch wurde festgestellt, dass ein Irrtum vorlag: nicht die angeblich zeugungsfähigen Tiere bekamen 2,5 Jubgtiere, sondern die Alttiere bis zu ihrem Sterben (Matrix - Anhang 2)
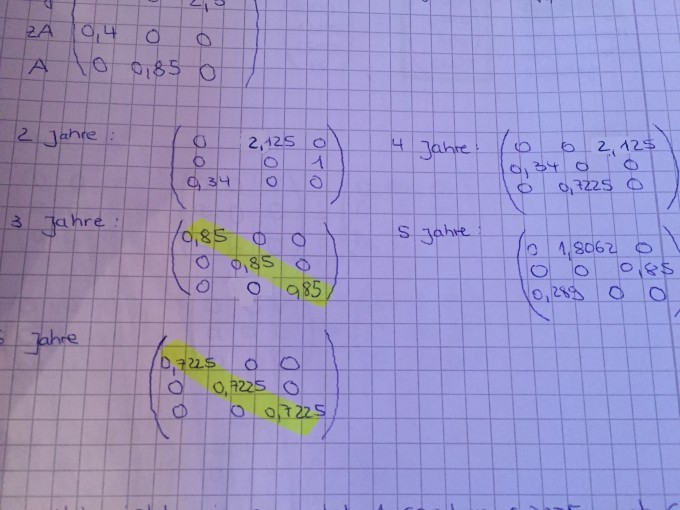
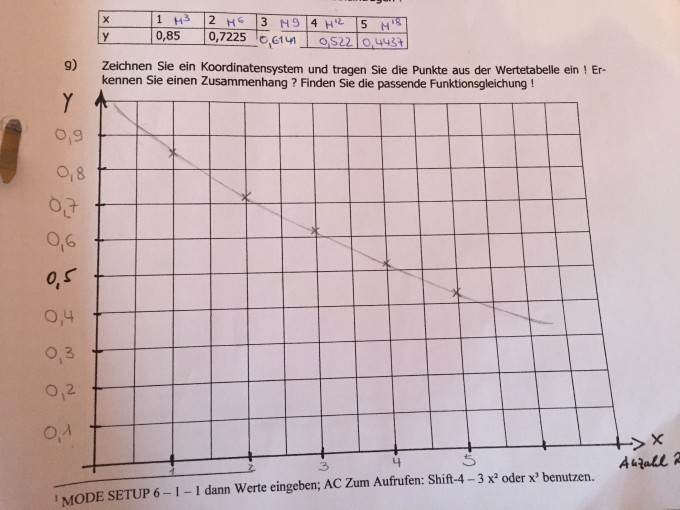
Von dieser Matrix ausgehen sollte ich nun die Populationen nach 2,3,4,5,6 Jahren ausrechnen. Dabei war auffällig, dass die Zahlen die in der Diagonalen stehen sich verringern (Anhang 3)
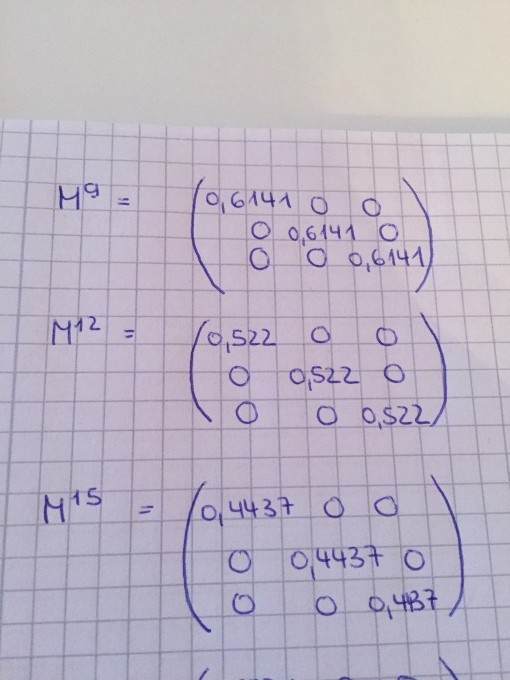
Nun sollte ich noch die Jahre 9,12,15 ausrechnen, da sich die Zahlen ja immer nach drei Jahren verringern. (Anhang 4)
Diese habe ich jetzt auch in ein Koordinatensystem eingezeichnet. Die Frage lautet nun: Ob ich einen Zusammenhang erkenne? Und dazu soll ich die passende Funktionsgleichung finden - wer kann mir da helfen (Anhang 5)