Konvergenzbereich einer komplexen Potenzreihe. Komplexe Zahlenebene: Aufgabe

Question

P51.

Brauche lösung und zwischenschritt.

Konvergenzbereich einer komplexen Potenzreihe. Komplexe Zahlenebene: Aufgabe

Comments

Wo genau liegt denn Dein Problem? (a) bis (c) sollte doch leicht zu machen sein - oder?

---

A und b bekomme ich hin.

Aber die c nicht wirklich weil ich nicht weiss wie man man lambda1 undz1 schreibt.

Ab da hab ich keine ahnung mehr.

Auch der summenzeichen macht mich fertig.

---

---

~plot~ f(x)=1 ~plot~

---

plot f(x)= 1 plot

Answer 1

(c) Um die Position der Punkte $z(\lambda_1,\lambda_2)=\lambda_1 z_1 + \lambda_3 z_3$ mit $\lambda_1, \lambda_2 \in[0,1]$ und $\lambda_1+\lambda_3=1$ zu finden, forme die Gleichung etwas um. Es ist

$$z=\lambda_1 z_1 + \lambda_3 z_3=\lambda_1 z_1 + (1-\lambda_1) z_3=z_3 + \lambda_1(z_1-z_3)$$

Sind $z_1$ und $z_3$ Positionen in der Gaußschen Zahlenebene, so ist obige Gleichung eine Gerade in eben dieser Ebene. Der Stützvektor ist $z_3$ und der Richtungsvektor ist $z_1-z_3$.

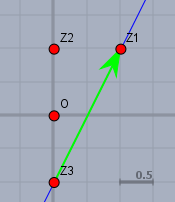
Und da sich der freie Parameter $\lambda_1$ nur im Intervall $[0,1]$ bewegt, ist die Menge aller $z$ in diesem Fall nur der grüne Pfeil - bzw. die Strecke mit den Enden $z_3$ und $z_1$.

(e) im zweidimensionale geht es analog.

$$z= \lambda_1z_1 + \lambda_2 z_2 + \lambda_3 z_3=(1-\lambda_2-\lambda_3) z_1 + \lambda_2z_2+\lambda_3 z_3$$

$$\space = z_1 + \lambda_2(z_2-z_1) + \lambda_3(z_3-z_1)$$

auch diese Gleichung sollte Dir aus der Vektorrechnung bekannt vorkommen. Es ist die Parameterform einer Ebene.

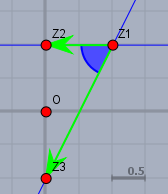
Und da bei bei beiden freien Parameter nur Werte >0 gemeint sind, befinden sich hier alle $z$-Werte zwischen den Pfeilen im Bereich des blau markierten Winkels. Die Forderung, dass ihre Summe 1 nicht überschreiten darf, führt dann zu einem Dreieck, innerhalb dem diese Werte liegen können.

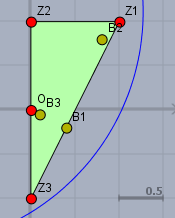
Das kennt man auch als baryzentrische Koordinaten.

(d)+(f) Ich habe oben in der Skizze auch einen möglichen Konvergenzkreis eingezeichnet (blau). Jeder Punkt auf einer Verbindungsstrecke zweier Punkte innerhalb des Kreises liegt zwangsläufgig wieder innerhalb des Kreises. Wenn die Funktion für die Werte $z_i$ konvergiert und alle Werte innerhalb eines Konvergenzkreises konvergieren, so müssen auch alle Funktionen mit Werten von $z$ konvergieren, die auf einer Verbindungsstrecke zwishen zwei konvergierenden Werten liegen.

Also lassen sich die Fragen in (d) und (f) jeweils mit 'Ja' beantworten.

Comments

Vielen Vielen Dank war sehr hilfreich :)