Ableitung der Umkehrfunktionen mit intervallen

Question

P55 bitte.

Ich komme so überhaupt nicht klar.

Hoffe ihr könnt mir weiter helfen.

Answer 1

Die zweite Ableitung ist die folgende:

$$\left(\frac{d}{dy}\right)^2f^{-1}(y) \\ =\frac{d}{dy}\left(\frac{d}{dy}f^{-1}(y)\right) \\ =\frac{d}{dy}\left(\frac{1}{f'\left(f^{-1}(y)\right)}\right) \\ =-\frac{1}{\left [f'\left(f^{-1}(y)\right)\right ]^2}\cdot \left(f'\left(f^{-1}(y)\right)\right)' \\ =-\frac{1}{\left [f'\left(f^{-1}(y)\right)\right ]^2}\cdot f''\left(f^{-1}(y)\right)\cdot \left(f^{-1}(y)\right)' \\ =-\frac{1}{\left [f'\left(f^{-1}(y)\right)\right ]^2}\cdot f''\left(f^{-1}(y)\right)\cdot \frac{1}{f'\left(f^{-1}(y)\right)} \\ =-\frac{f''\left(f^{-1}(y)\right)}{\left [f'\left(f^{-1}(y)\right)\right ]^3}$$

Comments

VIELEN Dank :)

Können sie mir bitte noch

Das mit vorzeichen und geometrische bedeutung erklären ?

---

Gerne :-) 

Wir haben dass f'(x)>0.

Die zweite Ableitung von f^-1(x) ist $$-\frac{f''(f^{-1}(y))}{[f'(f^{-1}(y))]^3}$$ Der Nenner ist positiv. Da vor den Bruch noch ein Minus Zeichen ist, ist das Vorzeichen der zweiten Ableitung von f^-1(x) das Gegenteil als das von f''(x).

Das Vorzeichen der zweiten Ableitung einer Funktion zeigt uns ob die Funktion konkav oder konvex ist.

Da die zweite Ableitungen einer Funktion f und dessen Inverse nicht das gleiche Vorzeichen haben, bedeutet es dass wenn wir f konkav ist dann ist die f^-1 konvex und umgekehrt. 

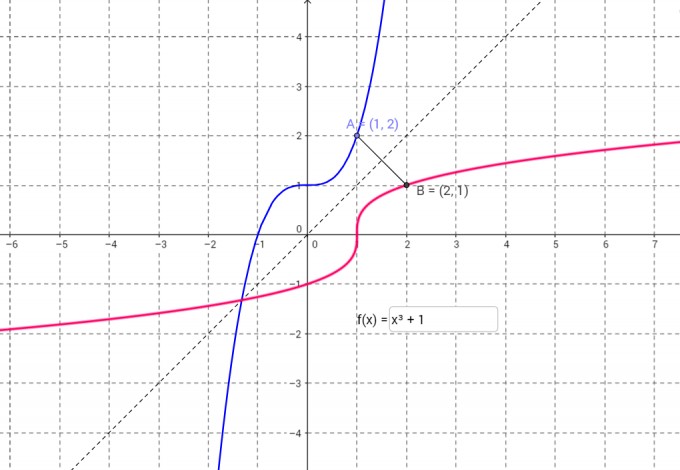
Wir sehen es zum Beispiel im folgenden Garphen: