DGL 1. Ordnung Substitution (x^2 + 1) y' + xy = 2x √(x^2 + 1)

Question

ich befinde mich weiterhin in der Vorbereitung für Mathe 1+2 und ich kann mich noch immer nicht mit der Substitution anfreunden. Ich komme beim unten genannten Beispiel nicht weiter.

Variablen trennen und dann Substitution u=-x^2 +1. Dafür sollte dann rauskommen

u=−x2−1 ⟶ du/dx=−2x

=−1/2∫1/u du =−1/2 ln(x² +1)

Aber wieso???? -1/2 du = x dx -> woher kommt das 1/u???

Ich hoffe jemand kann mir auf die Sprünge helfen ^^

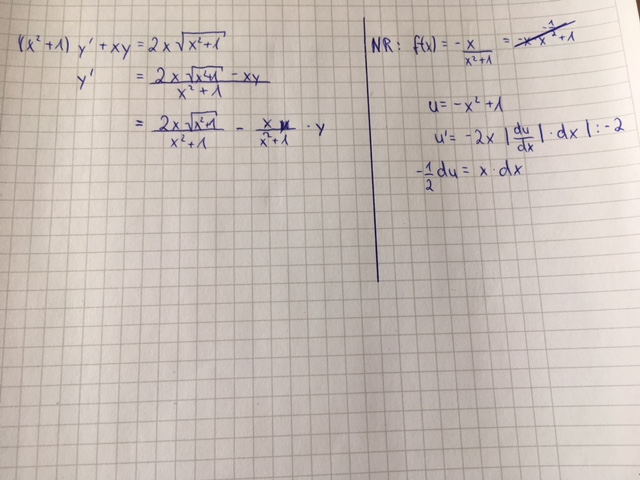
DGL 1. Ordnung Substitution (x^2 + 1) y' + xy = 2x √(x^2 + 1) 

Comments

Achtung: Du hast deine Variabeln gar nicht getrennt.

Solange rechts bei den vielen x ein y steht, kannst du noch nicht integrieren.

Bist du denn sicher, dass sich bei dieser DGL die Variabeln trennen lassen?

Warum denn das Minus bei u=-x² +1  ? 

---

naja das − x² +1 von − x/x²+1. Und wenn ich für y'= dy/dx schreibe und durch y teile habe ich rechts nur noch zwei Funktionen mit x. Aber gerne einen Lösungsweg vorgeben ^^ wie gesagt ich tue mich schwer mit Substitution.

---

EDIT: Ich wollte erst mal sicherstellen, ob du die Gleichung

 (x^2 + 1) y' + xy = 2x √(x^2 + 1)  

richtig abgeschrieben hast.

und: Ob Trennung der Variabeln zusammen mit deinem u  als Weg vorgeschlagen war.

---

Doch doch die ist korrekt abgeschrieben. Aber die Lösung alles unter vorbehalt :D

---

-------------------------------

Answer 1

Du kannst die Aufgabe auch ohne Substitution mit Variation der Konstanten lösen.

Du dividierst die DGL durch (x^2+1)

Du bekommst dann:

y' + (x/(x^2+1))  y = (2x)/(√x^2+1)

usw.

Comments

Würde es dir was ausmachen mir das einmal vorzurechnen. Ich habe jetzt so viel ausprobiert und stehe komplett auf dem Schlauch bei dieser Aufgabe :/

---

Wenn Du in Vorbereitung für Mathe 1+2 bist ,solttest Du "Variation der Konstanten kennen?

Hast Du mal in Deine Unterlagen geschaut?

Das habt Ihr bestimmt behandelt?

Was ist unklar?

---

bzw. würde mich viel mehr interessieren wie ich durch Substitution auf -1/2∫1/u du damit ich bei der Rücksubstitution -1/2 ln(-x² +1) bekomme :D

das wäre wirklich klasse.

---

Wie lautet  die Aufgabe genau (Photo)  möglich ??

Das mit der Substitution geht so gar nicht.

Habe es mal mit "Variation der Konstanten" gerechnet.

 

---

Ja das Ergebnis ist korrekt. Ich habe mir die Variation der Konstanten auch nochmal zu Gemüte geführt und das klappt alles soweit. Also dir erstmal vielen Dank für deine Mühe.