Wir betrachten ein rechteckiges Stück Land, im Westen begrenzt vom Längengrad 8° E, im Osten begrenzt von 11° E, im Norden begrenzt von 50° N und im Süden begrenzt von 45° N. Die Erde hat einen Aequatorradius von 6378,137 km und einen Polradius von 6356,752 km.
a) Wie lang ist die westliche Grenzline (Ellipsenbogen)?
b) Wie groß ist die Fläche (Integration des Ellipsenbogens)?
a)
Die Ellipse hat die Gleichung
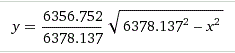
und sieht so aus: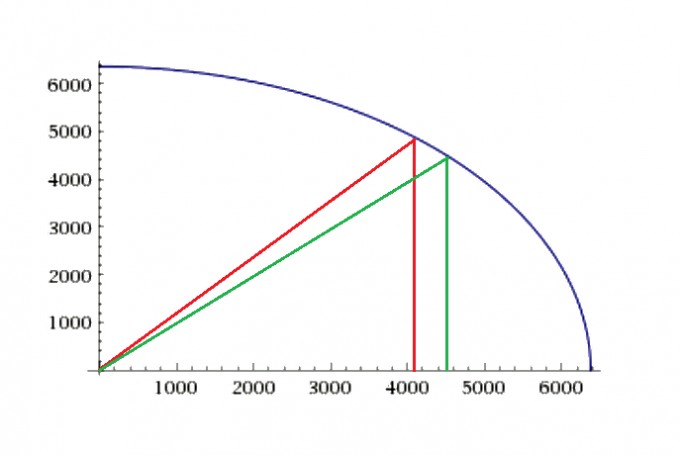
Die x-Werte bei den beiden Breitengraden 50° und 45° berechnen sich mit
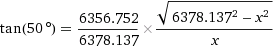
und
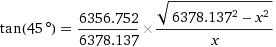
als 4091,7 km und 4502,44 km.
Die Länge des Ellipsenbogens in diesem Intervall beträgt:
d.h. 556 km, wobei es egal ist, ob man die westliche oder die östliche Grenze nimmt.
Die Lösung für Aufgabe b) würde mich auch noch interessieren.
Wobei ich hier eine Ungereimtheit entdeckt habe: Die Länge der nördlichen Grenze auf dem 50. Breitengrad ist so ausgerechnet 214,242 km, aber die geodätische Distanz zwischen den beiden nördlichen Eckpunkten, die ja kürzer sein soll, wird sowohl von Mathematica wie auch von Matlab mit 215,073 km angegeben.
Ich habe den Fehler gefunden: Der geodätische Breitengrad eines Ortes beim Ellipsoid ist nicht der Winkel zwischen der großen Halbachse und der Linie vom Mittelpunkt der Ellipse zu diesem Ort, wie oben gezeichnet, sondern der Winkel zwischen der großen Halbachse und der Senkrechten durch diesem Ort. Somit gilt bei diesem Beispiel für den Radius des Breitenkreises die Gleichung
d.h. der Radius ist 4107.86 km bei 50° und 4517.59 km bei 45° nördlicher Breite. Dann stimmen die Ergebnisse auch mit der kommerziellen Software überein.
Bei b) komme ich auf
d.h. 125 347 km2
Ein anderes Problem?
Willkommen bei der Mathelounge! Stell deine Frage einfach und kostenlos
