Berechnen Sie die folgenden Ausdrücke in der Form z = x + iy:
(a) i(i + 1)(i + 2) ;
(b) (4+2i) / (3+i)
(c) |(3+4i)10|
(d) 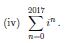
Hallo liebes Forum, ich komme mit dieser Aufgabe nicht zurecht und weiss nicht genau was ich hier machen soll. Ich weiss nur das es sich um komplexe Zahlen handelt. Habe hier auch shcon bisschen was versucht, für (a) habe ich -3+i erhalten, soll das dann in z = -3 + i geschrieben werden? Für (b) hätte ich noch z = 7/5 + 1/5i. Mit (c) und (d) weiss ich nichts anzufangen. Würde mich über Hilfe freuen. :D