Die Fakultät ist nichts weiter als die um 1 Einheit verschobene Gammafunktion:
x! = Gamma(x+1)
Gamma(x)=(x-1)!
Eigentlich total überflüssig, hier 2 verschiedene Namen zu verwenden!
Aber das ist geschichtlich so entstanden -> und Menschen sind nun mal eitel oder stur, und so haben sich 2 Lager gebildet.
Statt sich zu einigen und wissenschaftlich sauber die Algorithmen (Berechnungsvorschriften) zu sammeln wie unter
http://functions.wolfram.com/GammaBetaErf/Factorial/
(denn es gibt - Produkt-Algorithmen {nur für ganzzahlige Argumente}
- Summen {besser Reihen}
- Integrale
- hypergeometrische Funktionen
usw. )
sagen sture konservative (auch viele Lehrer): neee, die Fakultät gilt nur für ganze Zahlen.
Dabei kann man mit der
https://de.wikipedia.org/wiki/Stirlingformel
( Näherungsformel) mit Erweiterung um die Bernoulli-Zahlen eine beliebig genaue explizite Funktion (unendliche Summe) basteln und auch zeichnen, wie WolframAlpha &
http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php das machen :
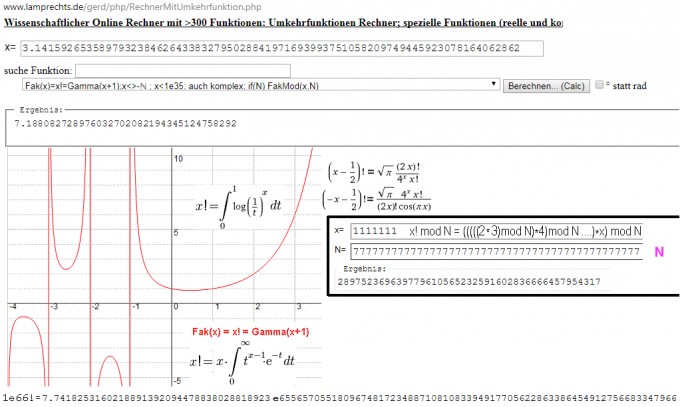
Beide können nicht nur sehr große Argumente, sondern auch komplexe Zahlen verarbeiten!
Das Besondere ist, dass es keine Nullstelle, sondern dafür viele Polstellen gibt. (bei -1, -2, ...)
Die Ergebnisse sind bis auf wenige Ausnahmen (ganzzahlige positive Argumente) immer irrational (unendlich viele Nachkommastellen).
Selbst Pi kann man so berechnen:
Pi = (Gamma(-1/2)/2)^2 = ((-3/2)!/2)² = Gamma(1/2)² = (-1/2)!²
Pi = (Fak(1/2)*2)^2 = (Gamma(3/2)*2)² {Fak(x)=x! }
...
Taschenrechner kann man vergessen -> da werden nur Näherungsfunktionen genommen, die oft nur 5 Nachkommastellen genau sind und bei 69! an ihre Grenzen stoßen!
Hier die Formel für 10 Nachkommstellen genau:
http://functions.wolfram.com/GammaBetaErf/Factorial/06/02/0002/
einfach für n Pi einsetzen.