ich habe eine tolle Frage:
Die Aufgabe:
Zeigen Sie, dass für jede natürliche Zahl n gilt:
Die Summe s(n)=n+(n+1)+(n+2)+...+(n+10) ist keine Primzahl.
Kann ich s(n) schreiben als
schreiben ?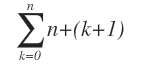
Wie drücke ist auf der anderen Seite der Gleichung ''ist keine Primzahl'' aus?
Die Zahl darf ja im Prinzip nicht durch 2 teilbar sein.