e funktion, ableitung und kurvendiskussion

Question

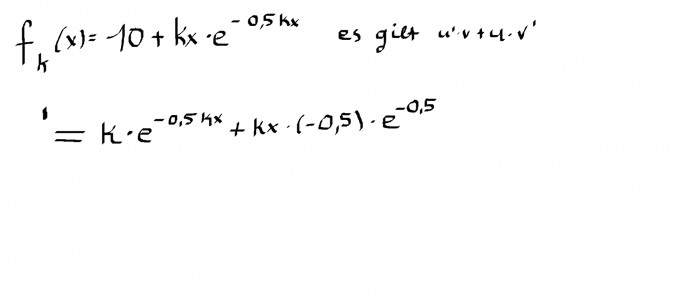
Warum fällt bei der Ableitung die 10 einfach weg. Kann mir das jemand erklären und mir dazu Übungsaufgaben dergleichen Art zur Verfügung stellen, ich will das kapieren... ruhig mit und ohne Parameter 3-4 Aufgaben..

Es gilt doch u'*v+u*v' , daher ist der Teil u 10+k*x, und beim ableiten, da bleibt doch u normal ... :/ Das verstehe ich nicht. Weil einmal u' abgeleitet wird und einmal u so stehen bleibt !

Answer 1

[10 + u(x)]' = [u(x) + 10]' = u'(x) + 0

Die 10 ist ein konstanter Summand und der fällt nach der Konstantenregel weg.

[c]' = 0

Answer 2

Konstanten werden immer zu Null abgeleitet. Einfach so merken. :)

Answer 3

Hi,

die Ableitung einer konstanten Funktion ist immer Null.

Stelle dir mal eine konstante Funktion vor. Z.B. \(f(x)=2\):

~plot~ 2 ~plot~

Die Ableitung gibt die Steigung deiner Funktion an. Und natürlich ist die Steigung einer konstanten Funktion an jeder Stelle 0, sonst würde sie ja mal steigen und/oder fallen.

Ist \(f(x)=c\) eine konstante Funktion, so gilt: \(f(x)'=c'=0\)

Aufgaben mit Lösungen:

https://www.brinkmann-du.de/mathe/aufgabenportal/p7_diff_int_t_01/p7_diff_int_t_01.htm

Hier noch eine von mir:

\(f(x)=k \cdot e^{1/k-x} \cdot x^2\)

Lösung:

[spoiler]

\( f'(x)=k \cdot x \cdot e^{1/k-x} \cdot (2-x) \) 

[/spoiler]