Hallo Anna-Lena,
In der Skizze habe ich das Viereck ABCD eingezeichnet. Die gelben Geraden sind die Winkelhalbierenden der vier Winkel im Viereck. Sie schneiden sich in den Punkten E bis H und bilden ein neues Viereck EFGH.
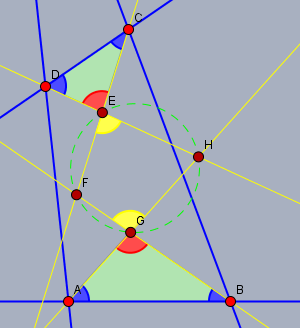
Die Winkelsumme in jedem Viereck ist 360°. Wenn man jeden der Winkel halbiert, so ist die Summe aller halben Winkel 180°. Also muss die Summe aller blauen Winkel in der Skizze auch =180° sein. Die Winkelsumme in den beiden grün markierten Dreiecken muss zusammen 360° betragen (2 Dreiecke a 180°). Ziehe ich von dieser Summe die 180° der blauen Winkel ab, so erhält man für die Summe der übrigen - also der roten - Winkel 180°. Da die roten Winkel die Scheitelwinkel der gelben sind, muss die Summe der gelben ebenfalls 180° betragen.
Ein Viereck, in dem die Winkelsumme zweier gegenüberliegender Winkel (hier der beiden gelben) gleich 180° ist, ist ein Sehnenviereck, hat also einen Umkreis.