Hallo Schmidt,
c)
f(x) = 1/5·x5 - x4
f '(x) = x4 - 4·x3
f "(x) = 4·x3 - 12·x2 ( = 0 ist die notwendige Bedingung für Wendestellen )
4·x3 - 12·x2 = 4·x2 · (x - 3) = 0
Satz vom Nullprodukt:
x = 0 ohne Vorzeichenwechsel von f "
x = 3 mit VZW von f " (hinreichende Bedingung für Wendestellen)
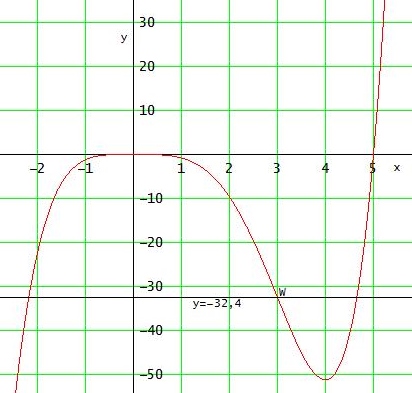
→ Wendestelle xw = 3
f(xw) = f(3) = -32,4
→ Wendepunkt W( 3 | -32,4 )
a) und b) analog
Nützlicher Online-Rechner:
https://matheguru.com/rechner/kurvendiskussion
Gruß Wolfgang