Einleitung:
Ringpermutation sind in der Kombinatorik Fälle wie:
Wie viele verschiedene Möglichkeiten gibt es 12 Leute, um einen runden Tisch zu setzen?
Es ist also eine Menge an Elemente, die im Kreis vertauscht werden sollen. Bei der Ringpermutation gibt es einen gravierenden Unterschied im Gegensatz zur gewöhnlichen Permutation:
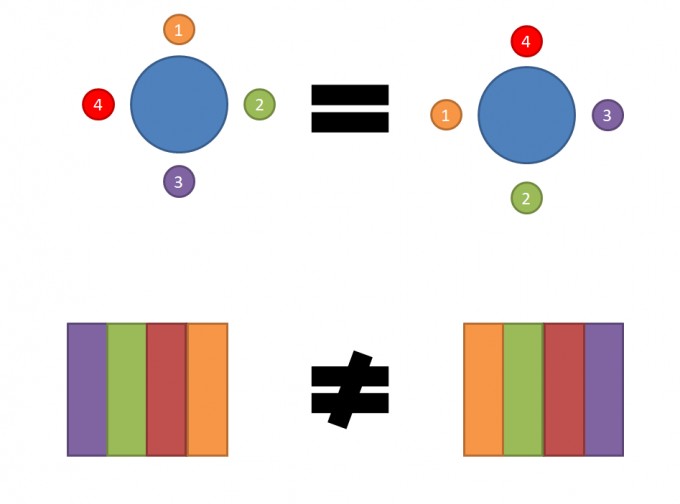
Wie man in diesem Schaubild sehr gut sehen kann gibt es bei der Ringpermutation, obwohl die Reihenfolge verändert wurde, keine wirkliche Veränderung. Rot sitzt nach einer Reihenfolgenänderung immer noch gegenüber von Grün und Lila immer noch gegenüber von Orange.
Wohingegen bei der gewöhnlichen Permutation (untere Grafik) nach einer Reihenfolgenänderung eine wirkliche Veränderung stattfindet. z. B. ist Lila nicht mehr neben Rot oder Orange nicht mehr neben Grün.
Bei der Ringpermutation mit vier Stühlen gibt es insgesamt 4 dieser Beispiele, in denen sich die Reihenfolge eigentlich nicht ändert. Eigentlich, weil man in manchen Aufgaben annimmt, dass eine Person z. B., weil die Sonne nur auf einem speziellen Platz scheint, an einem speziellen Platz sitzen will. Wir reden aber vorerst über Fälle, in denen die Reihenfolge nicht beachtet wird.
Wie beeinträchtigt das die Anzahl der Möglichkeiten?
Stellen wir uns dazu folgendes vor:
Wir haben den Auftrag 4 Personen auf einen runden Tisch aufzuteilen:
Nehmen wir an, wir sind in einem Raum, in dem kein Platz ein Vorteil gegenüber einem anderen hat (keine Fensterplätze, keine Lichtunterschiede etc.). Hier ist es also völlig egal, wo sich die erste Person hinsetzt. Da jeder Platz gleich ist, hat diese Person nur eine wirkliche Möglichkeit. Sobald sich diese Person gesetzt hat, ändert sich das aber. Jetzt spielt es eine Rolle, wo sich die nächste Person hinsetzt:
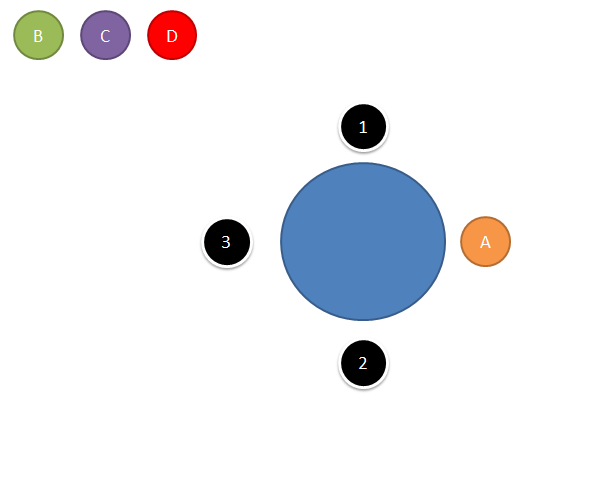
Sie kann sich also entweder rechts oder links von Person A hinsetzen oder ihr gegenübersitzen. Sie halt also 3 Möglichkeiten. Die Person B entscheidet sich dafür gegenüber von Person A zu sitzen. Person C hat jetzt nur noch 2 Möglichkeiten. Nämlich rechts oder links neben Person A. Die letze Person, also Person D hat nun nur noch eine einzige Möglichkeit sich zu setzen, da Person C sich für den Platz rechts neben Person A geschnappt hat.
In einer Formel kann man dieses Szenario so darstellen:$$(n-1)! \quad \text{oder} \quad \frac{n!}{n}$$Beispielaufgaben:
Wie viele Möglichkeiten gibt es, 12 Personen an einem runden Tisch zu verteilen?
Das ist nur nochmal zur Wiederholung und sollte nach der Erklärung oben kein Problem darstellen:$$(12-1)!=\frac{12!}{12}=39916800$$ Es gibt also 39916800 Wege, die Personen zu verteilen.
Der Kragen eines Lehrers ist geplatzt und er will das seine Klasse, bestehend aus 3 Jungen und 3 Mädchen, sich an einen runden Tisch verteilen, so dass jedes Mädchen abwechselnd neben einem Jungen sitzt, wie viele Möglichkeiten hat der Lehrer?
Hier müssen wir uns wieder daran erinnern, dass die erste Person, egal ob Junge oder Mädchen nur eine Möglichkeit hat, da es komplett egal ist, wohin sie sich setzt. Wenn sich ein Junge setzt, haben die anderen Jungen aber nur noch limierte Möglichkeiten, um die Reihenfolge zu befolgen:
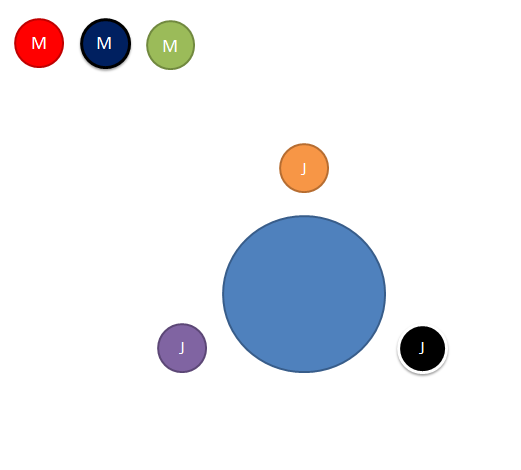
Der erste Junge (J) hat also eine Möglichkeit, die anderen beide haben 2 Möglichkeiten. Also haben wir schonmal \(1 \cdot 2!\) Möglichkeiten. Das erste Mädchen (M) hat jetzt drei verschiedene Möglichkeiten. Sobald sich das erste Mädchen setzt hat das andere 2 und das letze 1 Möglichkeit. Also haben wir \(3!\) Möglichkeiten. Daraus ergibt sich:$$2!\cdot 3!=12$$Es gibt also 12 Möglichkeiten, die Schüler aufzuteilen.
Nehmen wir an eine Gruppe von 3 Paaren (Junge & Mädchen) wollen sich an einen runden Tisch bei McDonalds setzen für ihr äußerst romantisches Candlelight dinner. Wie viele Möglichkeiten haben sie sich an einen runden Tisch zu setzen?
Das erste Paar setzt sich an zwei beliebige Stühle am Tisch. Sie haben nur eine wirkliche Möglichkeit sich hinzusetzen. Hier müssen wir Folgendes beachten:
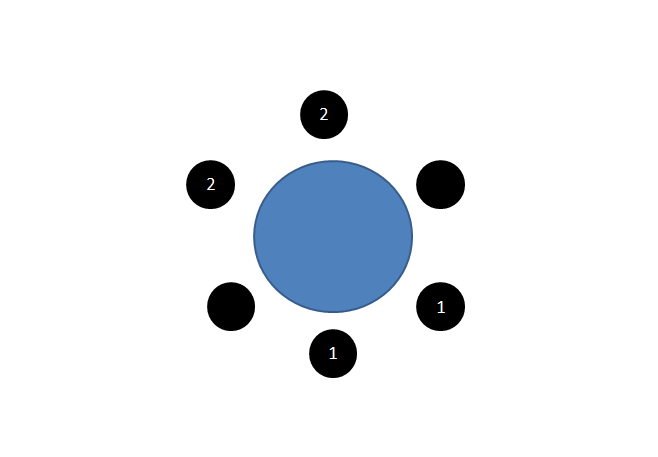
Die beiden Paare müssen sich immer nebeneinandersetzen, um das was in der oberen Grafik dargestellt ist zu vermeiden. Sie können sich also nur direkt nebeneinandersetzen. Wir betrachten jetzt für diesen Schritt nicht die einzelen Individuen sondern 3 Paare.
Das erste Paar hat wieder nur eine Möglichkeit, wohingegen das zweite zwei Möglichkeiten und das dritte nur noch eine hat, d.h. \(1 \cdot 2!\) Möglichkeiten für die Paare sich zu setzen. Jetzt können die Paare aber unter sich noch wechseln, hier gibt es also für jedes Paar \(2!\) Möglichkeiten. Und da wir 3 verschiendene Paare haben ergibt sich folgende Rechnung:$$2!\cdot (2!)^3=16$$
Wie viele Möglichkeiten gibt es, wenn 5 Jungen und 5 Mädchen alle getrennt an einem runden Tisch mit 10 Stühlen sitzen wollen?
Erinnern wir uns als das letzte Beispiel, wir sehen wieder nicht die einzelen Individuen, aber die ganze Gruppe als ein Element an. Wie viele Möglichkeiten hat die erste Gruppe sich zu setzen? Wie immer nur eine einzige, da es keinen wirklichen Unterschied gibt. Die zweite Gruppe hat auch nur noch eine Möglichkeit.
Sie können sich, aber wie beim letzen mal wieder innerhalb ihrer Gruppe neu verteilen. Die Rechnung ist also:$$1\cdot 1 \cdot (5!)^2$$
Ich hoffe, dass dieser Artikel euch gefällt und würde mich über Feedback sehr freuen.