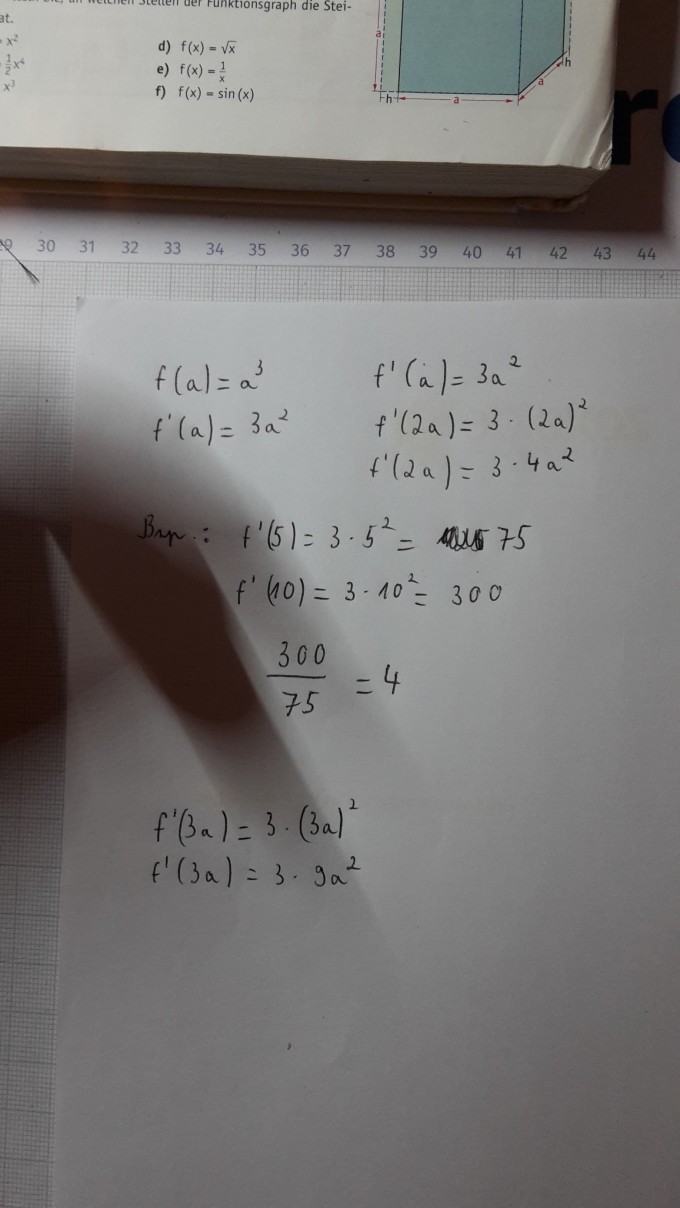Geometrische Deutung: Änderung der Kantenlänge eines Würfels

Question

da ich gerne eine Aufgabe aus meinem altem Mathebuch nacharbeiten würde, möchte ich hier um Rat fragen.

Aufg.: Betrachten Sie die Funktion, die jeder Kantenlänge a das Volumen des zugehörigen Würfels zuordnet. Bestimmen Sie die lokale Änderungsrate. Deuten Sie ihr Ergebnis geometrisch.

Zunächst habe ich die Funktion "aufgestellt" und dann hierzu die Ableitung gebildet. Meine Überlegungen waren, dass bei Verdoppelung der Kantenlänge sich die Änderungsrate vervierfacht, bei Verdreifachung verneunfacht etc. (s. Abbildungen).

Reicht das als geometische Deutung bzw. wie kann man das allgemein aufschreiben?

Answer 1

Ich denke, das ist eher so gemeint:

Wenn du die Kantenlänge um h vergrößerst, (so ist das ja auch in dem Bild)

kommen zum Volumen sozusagen 3 Scheiben dazu, die haben alle die Stärke h

und die Fläche a^2. Im Grenzfall ändert sich das Volumen also so,

dass es um 3*a^2 zunimmt.

Comments

Okay danke.

Aber wie meinst du das genau: Die hinzugekommen Scheiben durch die Verlängerung der Kantenlänge hätten alle die Stärke h.

---

Stärke bzw. Scheibendicke