Funktion für x<0 & x>0 auf Bijektivität überprüfen

Question

Leute!

Ich stehe gerade vor folgender Aufgabe und habe ein Problem. Und zwar bin ich mir sehr unsicher, wie ich diese Aufgabe lösen soll:

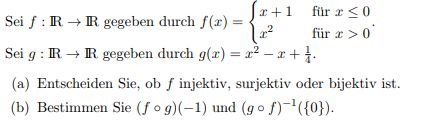
Da die Funktionsvorschrift von f ja von x abhängt, weiß ich nicht, wie man die ganze Funktion auf injektivität und co. überprüft...

ich habe es folgendermaßen überprüft, aber ich weiß nicht, ob das logisch ist...

Zu a)

Kann man die a) so beweisen? Oder habe ich etwas übersehen, womit der ganze Beweis dann zusammenfällt ? Ich bin mir da sehr unsicher, genau wegen der Fallunterscheidung.

Für eure Hilfe wäre ich hier an dieser Stelle echt dankbar.

zu b)

Hier ist mein Ansatz folgender:

Aber ich habe ein Problem bei (g ◦ f)^{−1}({0}). Ich weiß nicht, wie man diese Umkehrabbildung bildet und wie man diese berechnet... Meinen sie mit {0} einfach nur 0?

Auch hier wäre ich natürlich für jede Hilfe sehr dankbar.


Viele liebe Grüße

Domenik

Answer 1

Bei a): Die Funktion ist nicht Injektiv , denn es ist f(0,5)=0,25

und f(-0,75)=0,25 .

Solche Werte findest du leicht, wenn du den Graphen skizzierst.

surjektiv ist  f schon:   Für ein y>0 ist z.B.  f( √y) ) = y

und für y≤0 ist f(x-1)=y.

f(g(-1))  = f( 9/4)  =  81/16

(fog)^{-1} ({0}) = {-1}

Comments

hey, danke für deine Antwort!

Kurze Frage: Wenn f nicht für x>0 nicht injektiv ist, wie kann man anhand der Definition von Injektivität zu einem Widerspruch kommen? Weil anscheinend komme ich durch meinem "Beweis" zu der Schlussfolgerung, dass f doch injektiv ist. Findest du in meinem Beweis vielleicht irgend einen logischen Fehler? Weil wenn mein Beweis richtig sein würde, dann ergibt für mich die Definition von Injektivität wenig Sinn, denn dann könnte man "beweisen", dass jeder Graph injektiv ist.

Bei der Komposition hatte das Ergebnis wohl falsch abgeschrieben.

Wie hast du die Umkehrabbildung der Komposition gebildet? Ich weiß nicht wie es geht, da f ja 2 verschiedene Funktionsvorschriften hat...

freue mich auf deine Rückmeldung!

Liebe Grüße

Domenik