... weiss ich nicht was ich mit der Information "Die beiden äusseren gemeinsamen Tangenten gehen durch den Ursprung des Koordinatensystems." anfangen soll
Schau Dir mal folgende Skizze an:
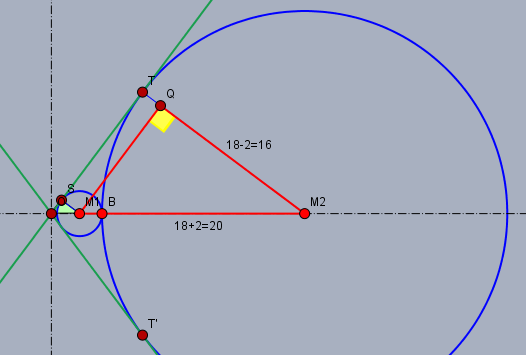
Dort siehst Du zwei (blaue) Kreise, deren Mittelpunkte auf der X-Achse liegen (die waagerechte Strich-Punkt-Linie). Die beiden gemeinsamen Tangenten (grün) schneiden sich im Ursprung \(O\) des Koordinatensystems. Wenn ich den Mittelpunkt des kleinen Kreises mit \(M_1\) und den des großen Kreises mit \(M_2\) bezeichne, dann sind ihre Koordinaten: $$\begin{aligned} M_1 &= \left( u \,| \, 0\right) \quad \text{ mit } u=|OM_1|\\ M_2 &= \left( u+20\, | \, 0\right) \end{aligned}$$ Die 20 ist die Summe der beiden Radien 2 und 18. Unbekannt ist also nur noch die X-Koordinate \(u\) von \(M_1\).
Ich habe parallel zu der oberen Tangente die Strecke \(M_1Q\) und senkrecht dazu den Radius \(M_2T\) eingezeichnet. \(T\) ist der Berührpunkt der Tangente mit dem Kreis um \(M_2\) und \(Q\) der Schnittpunkt der Parallelen durch \(M_1\) mit eben diesem Radius. Dann bilden die Punkte \(M_1\), \(M_2\) und \(Q\) ein rechtwinkliges Dreieck (rot), von dem wir zwei Seiten direkt ablesen können. Es ist \(|M_1M_2| = 2 + 18 = 20\) (s.o. Koordinate von \(M_2\)) und \(|QM_2|=18-2=16\), da die Parallele durch \(M_1\) genau um den Radius 2 zur Tangente versetzt ist. Ein ähnliches Dreieck findet man (grün markiert) bei \(\triangle OM_1S\). Wegen der Ähnlichkeit müssen alle Verhältnisse aller Strecken der beiden Dreiecke gleich sein. D.h.:
$$\frac{|OM_1|}{|SM_1|} = \frac{|M_1M_2|}{|QM_2|} = \frac{18+2}{18-2} = \frac54$$ \(|SM_1|\) ist aber der Radius des kleinen Kreises \(|SM_1|=2\). Daraus folgt $$|OM_1| = u = \frac54 \cdot 2 = 2,5 \\ |OM_2| = u + 20 = 2,5 + 20 = 22,5$$