Extremstellen mit Integralen

Question

Aufgabe:

Einen zum Zeitpunkt t=0 leeren Wassertank wird über ein Rohr Wasser zugeführt. Der Zufluss durch ein Rohr kann in den ersten 6 Stunden mit der Funktion z mit z(t) = t⁴-12t³+36t² ( t in Stunden, z(t) durchfluss in 100 l/h) modelliert werden. Ab dem Zeitpunkt t=4 wird dem Tank über ein ablassventil gleichmäßig pro Stunde 500 Liter Wasser entnommen.

A) berechnen sie die Wassermenge im Tank nach 4 Bzw. nach 6 Stunden

B) bestimmen Sie, zu welchem Zeitpunkt die Wassermenge im Tank maximal ist.

Problem/Ansatz:

A habe ich Problemos geschafft nur bei B komme ich nicht weiter. Habe weder noch einen ansatzt . Die Lösung ist anscheinend 5,6. wäre nett wenn ihr mir mit dem Rechenweg helfen würdet

Answer 1

b) bestimmen Sie, zu welchem Zeitpunkt die Wassermenge im Tank maximal ist.

t⁴ - 12·t³ + 36·t² - 5 = 0 → t = 5.601 h

Rechenweg ist schwierig. Die Gleichung ist numerisch zu lösen. Z.B. mit Intervallschachtelung.

Comments

Warum muss man denn bei der Funktion des zuflusses -5 machen und nicht bei dem Integral davon , also der Funktion der Wassermenge ?

---

Zunächst mal gilt

t⁴ - 12·t³ + 36·t² im Bereich von 0 bis 4. Hier hat man nur eine Nullstelle bei 0. Also läuft bis t = 4 Wasser zu.

t⁴ - 12·t³ + 36·t² - 5 gilt im Bereich von 4 bis 6. Hier hat man eine Nullstelle bei 5.601. Bis dorthin läuft mehr Wasser zu als ab. Danach läuft mehr wasser ab als zu und die Änderungsrate wird negativ. Damit hat man dort den Höchsten Füllstand.

Zeichne dir auch die Funktionen der Änderungsrate und des Füllstandes im gesamten Zeitraum aus zusammengesetzten Funktionen.

---

Die Zuflussfunktion sieht wie folgt aus:

---

Man könnte es auch so darstellen (was die Sache aber auch nicht einfacher macht, denn lästige Rechnungen habe ich weggelassen :-)):

Die Füllstandsmenge (Stammfunktion F von z mit z(0) = 0)  ist:

$F(t) = \begin{cases} t^5/5 - 3·t^4 + 12·t^3& 0≤ t ≤ 4 \\ t^5/5 - 3·t^4 + 12·t^3-5·(t-4)& 4 \lt t ≤ 6 \end{cases}$

F ist in t=4 stetig, aber nicht differenzierber.

Die Funktionsvorschrift der Ableitung in [0,6] \ {4} ist

$F'(t) = \begin{cases} t^4 - 12·t^3 + 36·t^2 & 0 ≤ t< 4 \\ t^4 - 12·t^3 + 36·t^2 - 5 & 4<t≤6 \end{cases}$

mit den Nullstellen

t₁ = 0   ;   t₂ = √(√(5 +9) + 3  ≈  5,601

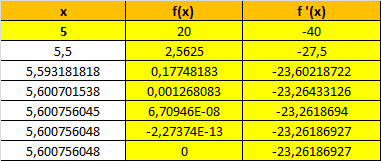
t₂   kann man auch näherungsweise (z.B. Newtonverfahren # ) berechnen, denn die Berechnung des genauen Wertes ist ohne Rechner nicht unlästig :-)

F"(t) =  4·t³ - 36·t² + 72·t  

 →   F"(t₂) ≈ - 23 < 0  →  Maximum bei t = 5,601 [h]  mit 250,5 Litern

[ An den Randstellen t=4 (204,8 l) und t=6 (249,2 l) sind es weniger]

-------

#  Newtonverfahren für F '(x) = x⁴ - 12·x³ + 36·x² - 5 = 0

$$x_{neu} = x_{alt} - \frac{f(x_{alt}}{ f ' (x_{alt})}$$mit dem naheliegenden Startwert 5 aus ] 4,6 ]  hat man x ≈ 5,6 schon nach 2 Schritten!