Also, ich weiss nicht konkret, wofür ich den brauche.
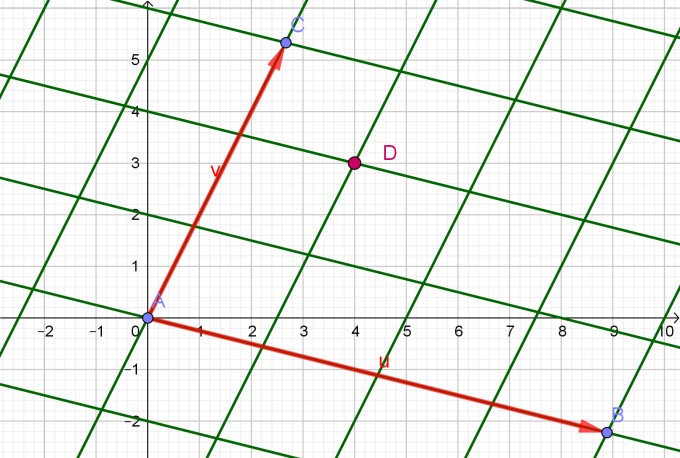
In der Abbildung siehst du einen Punkt D, der im "üblichen" Koordinatensystem mit \( \begin{pmatrix} 1\\0 \end{pmatrix} \) und \( \begin{pmatrix} 0\\1 \end{pmatrix} \) als Basisvektoren die Koordinaten (4;3) hat. In einem anderen Koordinatensystem, in dem die beiden rot eingezeichneten Vektoren u und v die Basis bilden, hätte der gleiche Punkt die Koordinaten (1/4 ; 2/3).
Der Wechsel der verwendeten Basis führt in der Regel zu neuen Koordinaten des gleichen Punktes.
Was ist die Übergangsmatrix ?
Die braucht man, um aus den alten Koordinaten die sich aus dem Basiswechsel ergebenden neuen Koordinaten zu berechnen.