Hallo Mathegemeinde,
ich habe ein Problem mit einer Umformung einer Doppelsumme.
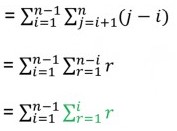
Der Schritt von Gleichung 1 auf Gleichung zwei ist mir (hoffentlich) klar, es erfolgt ein Indexshift
indem +i in der Rechnung und -i beim Start- und Endindex gerechnet wird.
Die Variable j, welche dann über bleibt, wird in r umbenannt (r beginnt ja nun bei 1 und endet quasi bei n-i, richtig?).
Nun mein größeres Problem, von Gleichung 2 auf Gleichung 3, also von schwarz zu grün, wie kann das entstehen?
Ich habe probiert, konkrete Zahlen einzusetzen, verstehe aber leider nicht, wie das mit der Doppelsumme dann aufgeschrieben wird, weil wir ja nur eine einzelne Variable haben (und nicht wie in Gleichung 1 ein j und ein i).
Ich hoffe, jemand kann mir das vielleicht auch an einem konkreten Zahlenbeispiel erklären, ich wäre euch sehr dankbar!!
!