Gegeben sind die rechtwinkligen Dreiecke ABC und DEF.
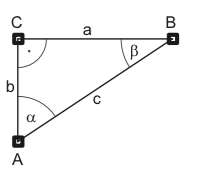
a) Ergänze für das Dreieck ABC:
\(\begin{aligned} \sin (\alpha) &=- \quad \sin (\beta)=-\\ \cos (\alpha) &=-\quad \cos (\beta)=-\\ \tan (\alpha) &=-\quad \tan (\beta)=-\end{aligned}\)
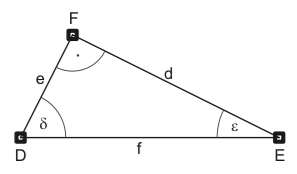
b) Ergänze für das Dreieck DEF:
\(\begin{array}{ll}{\sin (\delta)=-} & {\sin (\varepsilon)=-} \\ {\cos (\delta)=-} & {\cos (\varepsilon)=-} \\ {\tan (\delta)=-} & {\tan (\varepsilon)=-}\end{array}\)