Grundsätzlich musst du immer 1/ verwenden, wenn du aus einem negativen Exponenten einen positiven machen willst. Das liegt an der Definition, die man bei negativen Exponenten verwendet.
Nur gibt's in der Regel einen Trick zum Abkürzen.
In deinen Beispielen:
Ausführliche Variante:
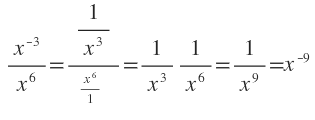
Abkürzung: mit dem - den Nenner direkt in den Zähler holen
= x-3 * x- 6 = x - 9 Bei Buchstaben in der Basis versucht man oft die Nenner der Brüche wegzubringen.
2. Beispiel: ausführliche Variante:
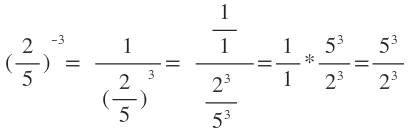
Abkürzung: Kehrwert nehmen und dafür hoch 3 schreiben, danach noch hoch 3 auf Zähler und Nenner anwenden
=(5/2)^3 = (5^3)/(2^3) = 125/8
Bei Zahlen hat man am Schluss gern einen Bruch. Das ist genauer als eine gerundete Dezimalzahl