Bestimmen Sie das Volumen des abgebildeten Körpers:

Question

Aufgabe:

Bestimmen Sie das Volumen des abgebildeten Körpers:

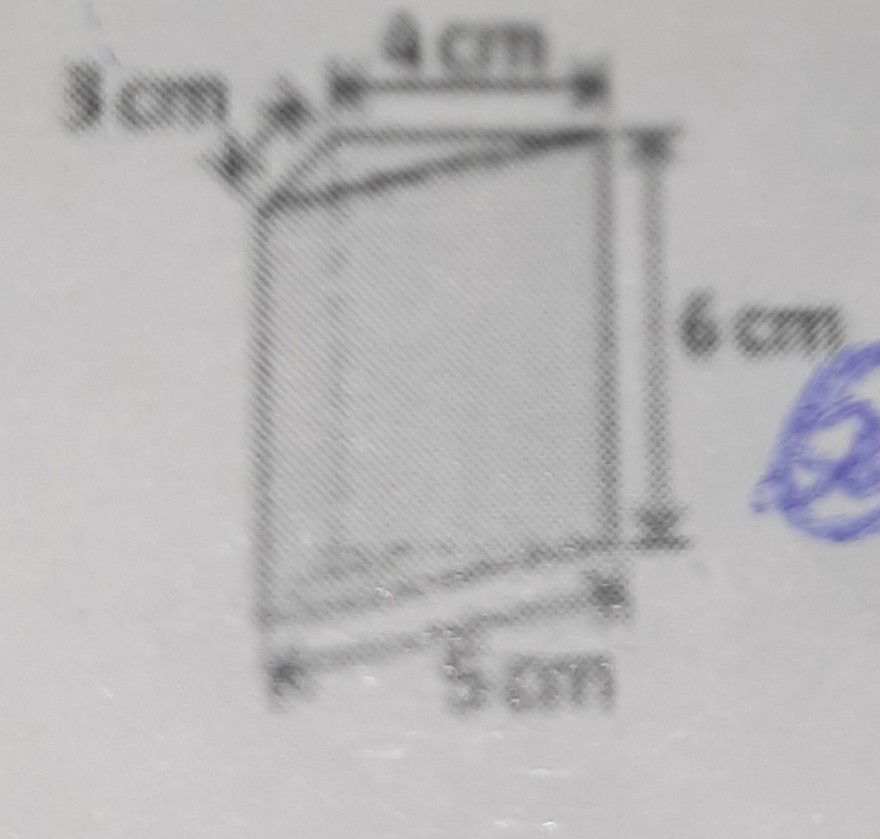
Problem/Ansatz:

Das Volumen lässt sich durch folgende Formel berechnen:

V = G * h und die Grundfläche eines Dreiecks durch die Formel:

A = 1/2 * g * h, jedoch ist die Höhe des Dreiecks nicht bekannt.

Ich habe im Internet recherchiert und habe herausbekommen, dass die Formel bezüglich der Berechnung der Höhe vom rechtwenkligen Dreieck:

Kathete * Kathete / Hypotenuse

Dies angewendet erhält man folgendes:

A = 1/2 * 5 cm * (3 cm * 4 cm / 5 cm) = 1/2 * 5 cm * 12/5 = 6 cm²

Jedoch steht in den Lösungen etwas anders:

A = 1/2 * 5 cm * 3 cm = 15/2 cm²

Wieso ist hier dann die Höhe anders?

Answer 1

Die Bildqualität ist sehr verschwommen.

Es handelt sich um ein rechtwinkliges Dreieck (Hälfte eines Rechteckes), weshalb A_Dreieck  = (3 * 4)/2 cm² = 6 cm² .

Mit der angegebenen Höhe ergibt sich V = 6 cm² * 6 cm = 36 cm³ .

Da scheint wohl die Lösung einen Fehler zu haben.

Answer 2

A = 1/2 * 3 cm * 4 cm = 6 cm^2

wäre richtig.

Comments

Ja, aber wieso 3 cm als Höhe und nicht 12/5 cm?

---

Für rechtwinklige Dreiecke ist die Höhe des Dreiecks für die Fläche uninteressant. Kombinierst du zwei gleiche rechtwinklige Dreiecke, so erhältst du ein Rechteck. Daher ist die Fläche des rechtwinkligen Dreiecks mit den Katheten X und Y genauso groß, wie die Hälfte der Fläche des durch die Katheten X und Y aufgespannten Rechtecks.

---

@NeverGiveUp:

Für rechtwinklige Dreiecke ist die Höhe des Dreiecks für die Fläche uninteressant.

Eigentlich nicht, denn: Ein Dreieck hat nicht "die Höhe", sondern immer deren drei, die auch gleich lang sein können. In einem rechtwinkligen Dreieck lässt sich immer eine beliebige Kathete als Höhe und die jeweils andere als Grundseite wählen.

@Andreaskreuz:

Ich habe im Internet recherchiert und habe herausbekommen, dass die Formel bezüglich der Berechnung der Höhe vom rechtwenkligen Dreieck:
Kathete * Kathete / Hypotenuse

Gib mal die Quelle an!

---

---

Eigentlich nicht, denn: Ein Dreieck hat nicht "die Höhe", sondern immer deren drei, die auch gleich lang sein können. In einem rechtwinkligen Dreieck lässt sich immer eine beliebige Kathete als Höhe und die jeweils andere als Grundseite wählen.

Das stimmt.

Eigentlich wollte ich darauf hinaus, dass der Fragesteller hier nicht zwangsweise zuerst die Höhe und danach mit der allgemeinen Flächeninhaltsgleichung für Dreiecke (Grundfläche * Höhe) die Fläche berechnen müsste, sondern noch einfacher über den Bezug zu einem Rechteck hätte gehen können.

Dabei sind die Katheten des rechtwinkligen Dreiecks natürlich bereits 2 der 3 möglichen Höhen des Dreiecks, weshalb ich mit meiner Aussage dahingehend natürlich falsch lag.

Answer 3

Hallo,

es geht hier um ein Dreiecksprisma

V = G *h                h =6 cm

       G : rechtwinkliges Dreieck           G = 3*4/2   = 6cm²

V = 6 *6        -> 36cm³

die Seitenlängen des Dreieckes bilden ein pythagoräisches Tripel

c²=a²+b²         5²=3²+4²      25=25 und damit ist das Dreieck rechtwinklig

( Auch Musterlösungen können Fehler beinhalten)

Comments

Ja, die Musterlösung ist falsch, doch das Internet hat sich nicht geirrt, die Höhe der 5 cm langen Seite beträgt 3*4/5 cm = 12/5 cm, nun war das nicht gefragt, doch falsch ist es ja nicht.