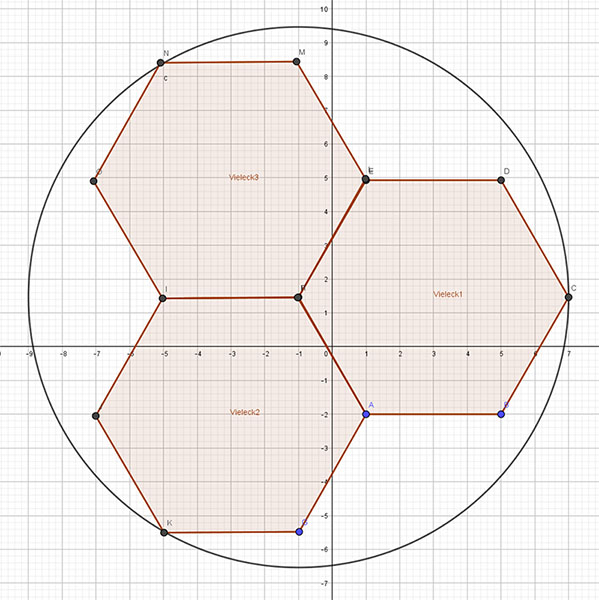
Habe A = 8* Pi = 25,1 raus, bei Seitenlänge 1. Entspricht 9,67 mal dem Sechseck.
Das Sechseck wird 6 mal überstrichen.
Dann noch das Stück zwischen Kreis und Secheck 6-mal.
Der ganze Kreis hat die Fläche 4 Pi.
Davon 3 Sechsecke abziehen und durch 3 teilen.