Berechnen Sie die Extrempunkte der Funktion

Question

Aufgabe:

Berechnen Sie die Extrempunkte der Funktion:

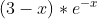
Problem/Ansatz:

Dabei kommt man ja entweder auf:

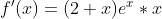
oder auf:

Und da kommt die falsche Ableitung für f‘‘(x) raus, wenn ich das x ausklammer. Gibt es da eine bestimmte Regel?

Vielen Dank für eure Antworten :)

Comments

Deine Ableitungsvorschläge sind nicht richtig. Wie hast du sie berechnet?

Answer 1

Aloha :)

Die Funktion$$f(x)=(3-x)\cdot e^{-x}$$leitest du am schnellsten mit der Produktregel ab:$$f'(x)=\left[\underbrace{(3-x)}_{=u}\cdot \underbrace{e^{-x}}_{=v}\right]'=\underbrace{(-1)}_{=u'}\cdot \underbrace{e^{-x}}_{=v}+\underbrace{(3-x)}_{=u}\cdot \underbrace{(-e^{-x})}_{=v'}=(x-4)e^{-x}$$Da die $e$-Funktion immer positiv ist, kann nur die Klammer zu null werden, und das tut sie für $x=4$. Die Art des Extremums bestimmen wir mit Hilfe der zweiten Ableitung:$$f''(x)=\left[\underbrace{(x-4)}_{=u}\cdot \underbrace{e^{-x}}_{=v}\right]'=\underbrace{(1)}_{=u'}\cdot \underbrace{e^{-x}}_{=v}+\underbrace{(x-4)}_{=u}\cdot \underbrace{(-e^{-x})}_{=v'}=(5-x)e^{-x}$$Wegen $f''(4)=(5-4)e^{-4}>0$ handelt es sich bei dem Extremum um ein Minimum.

Answer 2

Dabei kommt man ja entweder auf... oder auf...:

Weder noch. Auch in den Ableitungen hat der exponentielle Teil nach wie vor die Form

e hoch MINUS x.