Aufgabe zu Summenzeichen

Question

Aufgabe:

Habe ein Problem bei dieser Aufgabe bzgl. der Summenzeichenregeln und der Beweisung der folgenden Aufgabe:

Das arithmetische Mittel von a1, a2, ..., an ist definiert als:

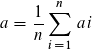
Zeige das :

Text erkannt:

$\sum \limits_{i=1}^{n}(a i-a)^{2}=\sum \limits_{i=1}^{n} a i^{2}-n \cdot a^{2}$

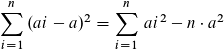
Anmerkung: Mit a ist natürlich ā gemeint

Auf eine schnelle Antwort würde ich mich freuen

Mfg GabbaGauß

Text erkannt:

$\sum \limits_{i=1}^{n}(a i-a)^{2}=\sum \limits_{i=1}^{n} a i^{2}-n \cdot a^{2}$

Text erkannt:

$a=\frac{1}{n} \sum \limits_{i=1}^{n} a i$

Answer 1

Hallo,

Willkommen in der Mathelounge.

In Deiner Fragestellung geht es mit $a$ und $\overline a$ etwas durcheinander. Ich denke Du möchtest zeigen, dass $$\sum_{i=1}^n (a_i - \overline a)^2 = \sum_{i=1}^n a_i^2 - n \overline a^2$$Dazu brauchst Du nur den linken Term nach der binomischen Formel auflösen. Es ist$$\begin{aligned} \sum_{i=1}^n (a_i - \overline a)^2 &= \sum_{i=1}^n \left( a_i^2 - 2a_i \overline a + \overline a^2\right) \\ &= \sum_{i=1}^n a_i^2 - \sum_{i=1}^n 2a_i\overline a + \sum_{i=1}^n \overline a^2 \\ &= \sum_{i=1}^n a_i^2 - 2 \overline a\sum_{i=1}^n a_i + n \overline a^2 \\ &= \sum_{i=1}^n a_i^2 - 2 n\overline a \cdot \frac 1n \sum_{i=1}^n a_i + n \overline a^2 \\ &= \sum_{i=1}^n a_i^2 - 2 n\overline a^2 + n \overline a^2 \\ &= \sum_{i=1}^n a_i^2 - n \overline a^2 \end{aligned}$$Alles klar?

Comments

Ja vielen danke

---

Hallo,

Willkommen in der Mathelounge.