Hallo,
Ich unterstelle, dass die Zahlen an dem \(\mathbb F_3^2\) nur Indizes und keine Dimensionen sind, sonst macht die Aufgabe IMHO keinen Sinn.
Der Kern einer linearen Abbildung \(f\) sind alle Punkte \(x\) für die gilt:$$f: \quad A \cdot x = 0$$und da \(\det(A) \ne 0\), ist das in diesem Fall nur der Nullvektor \(\ker(f) = \vec 0\) und seine Dimension ist \(\text{dim}(\ker(f))=0\). Aus dem selben Grund ist das Bild der gesamte \(\mathbb R^3\); die Dimension des Bildes ist also \(\text{dim}(\text{im}(f)) = 3\).
Im Falle von \(g\) ist der Kern die Ursprungsebene, die senkrecht auf dem Vektor \(n = \begin{pmatrix}1\\ 1\\ 1\end{pmatrix}\) steht und das Bild die Ursprungsgerade in Richtung \(r = \begin{pmatrix}1\\ 0\\ 0\end{pmatrix}\) (die X-Achse im Bild unten). Die Dimension des Kerns ist also \(\text{dim}(\ker(g))=2\) und das Bild hat somit die Dimension \(\text{dim}(\text{im}(g))=3-2=1\).
Zum Verständnis:
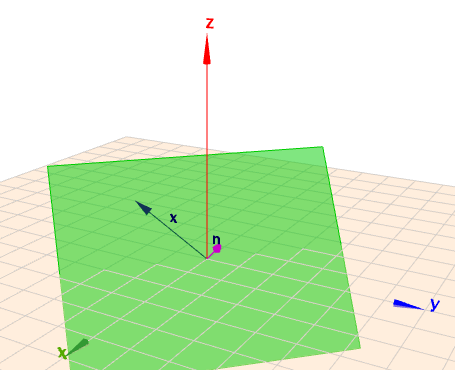
Wenn Du irgendeinen Vektor - z.B. das \(x\) - nimmst, der in der grünen Ebene \(E_k\) liegt, so wird das Produkt $$\begin{pmatrix}1& 1& 1\\ 0& 0& 0\\ 0& 0& 0\end{pmatrix} \cdot x = \vec 0, \quad x \in E_k$$da immer \(x \perp n\) gilt. Nimmst Du dagegen einen beliebigen anderen Vektor, so wird dieser immer auf die X-Achse abgebildet, da nur die erste Zeile der Matrix \(B\) Koeffizienten \(\ne 0\) enthält. Die X-Achse ist somit das Bild von \(g\).
Gruß Werner