Bestimme die Größe des Waldstücks in Hektar.

Question

Aufgabe:

Schüler einer 10. Klasse wollen die Größe des dreieckigen Waldstücks vor ihrer Schule bestimmen. Sie ermitteln dessen Seitenlängen mit 370 m, 244 m und 169 m. Bestimme die Größe des Waldstücks in Hektar.

Answer 1

Verwende den Satz des Heron:

https://de.wikipedia.org/wiki/Satz_des_Heron

Answer 2

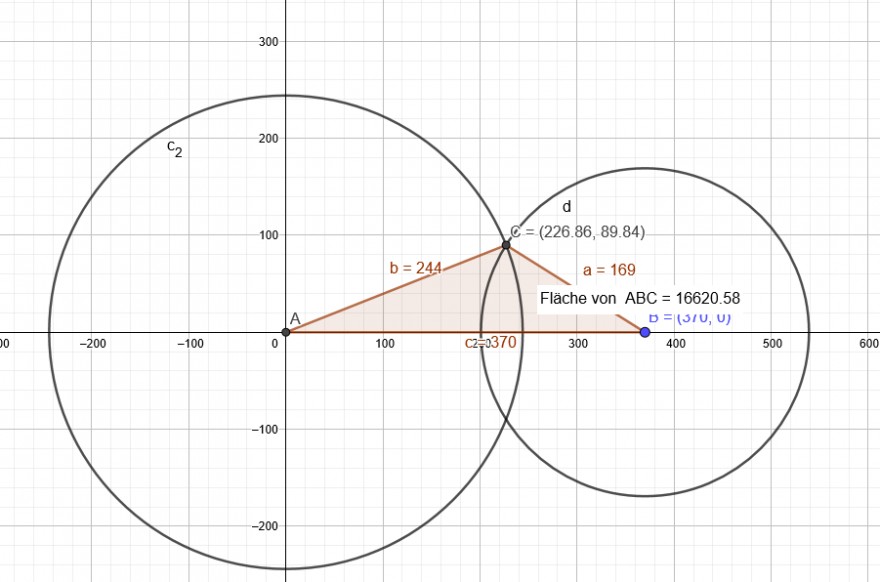
Kreis um A(0 |0) mit r =244

x^2+y^2=244^2

Kreis um B(370 |0) mit r =169  

Diese Kreise schneiden sich in C(226,86|89,84)

Dreiecksfläche: \( \frac{370*89,84}{2} \)=16620,4( Ich weiß nicht, warum die Werte nach dem Komma nicht übereinstimmen.)

Der Wald ist 16620,4\( m^{2} \) = 1,66204 ha groß.