Wie löst man Textaufgaben zur Ebene und Parameterform?

Question

Aufgabe:

Ein Segelschiff N segelt bei Windstärke 7. Die Segelcrew spürt eine Krängung nach Steuerbord. Die Eckpunktepunkte sind A (2|1|2), B (10|6|3), C ( 6|7|13) und D (2|4|11)    ...( 1 Einheit entspricht 10m )

Nr. 1 Beschreibe das Grosssegel durch eine geeignete Ebene, Parameter, Normal und Koordinatenform ( Bei einer Windstärke 7 kann bei der Darstellung des Segels von einer Ebene ausgegangen werden)

2. Wegen dem Bernoullieffekt drückt der Wind das Schiff in eine Richtung senkrecht zur Segelfläche. Bestimme die Richtung, die rechtwinklig zur Segelfläche steht.

3. Berechne den Neigungswinkel des Schiffes zur Wasserfläche.

4. Eine Signalrakete wird abgeschossen. Der Startpunkt liegt bei R ( 14|0|1) und die Richtung der Flugbahn ist v = (-2/4/15). Weise rechnerisch warum der Großsegel unbeschädigt ist

 5. Eine Möwe befindet sich im Punkt (30|-49|18) Berechne den Abstand der Möwe zum Segel. Die Gerade lautet g: x= (3/1/0) + r(1/-1/0). Ein Fischerboot hat ein Netz ausgeworfen. Die Ebene F: [ x-(6/0/0)]*(1/2/-3)=0 beschrieben

6. Überprüfe ob der Fischernetz auf der Route des Schiffes liegt

7. Im Punkt Q(4|0|0) ändert der Skipper die Richtung um den Aufprall zu vermeiden und wählt eine Richtung parallel zum Fischernetz. Bestimme die Geradengleichung.

Problem/Ansatz:

Sehr Sehr schwere Aufgabe zu Ebene, Parameter, Normal und Koordinatenform.

Answer 1

Hallo

Parameterform einen Aufbukt wählen z,B, A, und 2 Richtungsvektoren AB und AC z. B.

dann  in Koordinatenform umformen oder ax+by+cz=d  3 Punkte einsetzen und a,b,c,d bestimmen bestimmen.

Gruß lul

Comments

Vielen Dank. Wie löst man die Aufgabe 5. ?

---

Hallo

a) Abstand Möge- Segel. die Gerade durch die Koordinate der Möge mit Richtungsvektor normal zum Segel schneidet des Segel, dann Abstand der Punktes, oder Koordinatengleichung iNormalform gibt den Abstand zu 0, dann Abstand der Möge zu 0 und Differenz .

Den 2 ten Teil versteh ich nicht ganz, da schein was durcheinander was hat "Die Gerade lautet g: x= (3/1/0) + r(1/-1/0). Ein Fischerboot hat ein Netz ausgeworfen. Die Ebene F: [ x-(6/0/0)]*(1/2/-3)=0 beschrieben" mit Möge und Segel zu tun?

Gruß lul

Answer 2

Bei solchen Aufgaben immer eine Zeichnung machen

Merke:Eine Ebene ist durch 3 gegebene Punkte A,B und C eindeutig bestimmt.

Dreipunktgleichung der Ebene E: x=a+r*(b-a)+s*(c-a)

A(2/1/2) → Ortsvektor a(2/1/2)

B(10/6/3) → Ortsvektor b(10/6/3)

C(6/7/13) → Ortsvektor c(6/7/13)

D(2/4/11) → Orsvektor d(2/4/11)

E: x=(2/1/2)+r*[(10/6/3)-(2/1/2)]+s*[(6/7/13)-(2/1/2)]

E: x=(2/1/2)+r*(8/5/1)+s*(4/6/11)

Normalenvektor mit meinem Graphikrechner (GTR,Casio) → n(49/-84/28) dividiert durch 7

n(7/-12/4)

1) kann man über das Vektorprodukt (Kreusprodukt) a kreuz b=c ausrechnen

2) über das Skalarprodukt a*b=ax*bx+ay*by+az*bz

1) u*n=ux*nx+uy*ny+uz*nz=0

2) v*n=vx*nx+vy*ny+vz*nz=0

wir setzen nz=1

1) ux*nx+uy*ny=-1*uz

2) vx*nx+vy*ny=-1*vz

Hinweis:Der Punkt D(2/4/11) → d(2/4/11) liegt auf der Ebene bei r=-3/7 und s=6/7

Normalengleichung der Ebene E: (x-a)*n=0

[(x-(2/1/2)]*(7/-12/4)=0

ergibt die Koordinatengleichung der Ebene E: a*x+b*y+c*z+d=0

Den Rest mußt du selber schaffen,weil mir das zu viel Arbeit ist,die man mir nicht bezahlt.

Infos,vergrößern und/oder herunterladen

Text erkannt:

az) genoanen. Man kann aber anch den
"leichgesetzt ersibt: $(b x / b y / b z)=(a x / a y / a z)+1 *(n x / x y / n z)$
Hinveis:A(ax/ay/az) sind die $x, y$ und z Koordi naten der vektor-
BC. Abstand von 2 Punkten in Raun $d-\sqrt{(x 2-x 2)^{2}+(y 2-y 1)^{2}+(x 2-z 1)^{2}}$
Hier ist der "Betrag" von d zu nehth Skalar produkt a a b-ax tehen die beiden Vektoren a und b "senkrecht" aufeinander,so ist das Skalarprodukt gleich a18o a*b-ax* bx $+a y^{*}$ by $y$
der Ebene Begeben sind die 3 Punkte a $(\mathrm{ax} / \mathrm{ay} / \mathrm{az})$ und $\mathrm{b}(\mathrm{b} \mathrm{x} / \mathrm{by} / \mathrm{bz})$ und $\mathrm{c}(\mathrm{cx} / \mathrm{cs}$
$c(c x / c y / c z)$
vekte der Ebeng $\varepsilon: t-\vec{a}+r * \vec{u}+s \cdot \vec{v}$
$\overrightarrow{ }^{11} \mathrm{t} \vec{\sigma}_{-} \bar{b}-{\vec{a}}^{\overrightarrow{2}}$ und $\vec{v}=(\overrightarrow{\mathrm{c}}-$
Nornalengleichung der Ebene $\quad E:(\vec{x}-\vec{a}) * \vec{n}=0 \quad \mathrm{n}(\mathrm{nx} / \mathrm{n}$
Der Normalenvektor steht "senkrecht" auf den Richtungsvektoren $\vec{d}$ und $\vec{t}$ es gilt:

Gieichungen mit 2 Unbekante ar
hung der Bbene $\mathrm{R}$ : $\mathrm{a}^{*} \mathrm{x}+\mathrm{b}^{*} \mathrm{y}+\mathrm{c}^{*} z+\mathrm{d}=0$
1) d-0 die Ebene senau durch den Ursprung
3) verläuft "paralle1 zur $x$ -Achse "aur $y$ -Ahs
4) z-Achse"
Kreuzprodukt) eht senkrechte auf den Yek-
Hierait kann man den "Normalenvektor" für die Ebene bestinaen 7

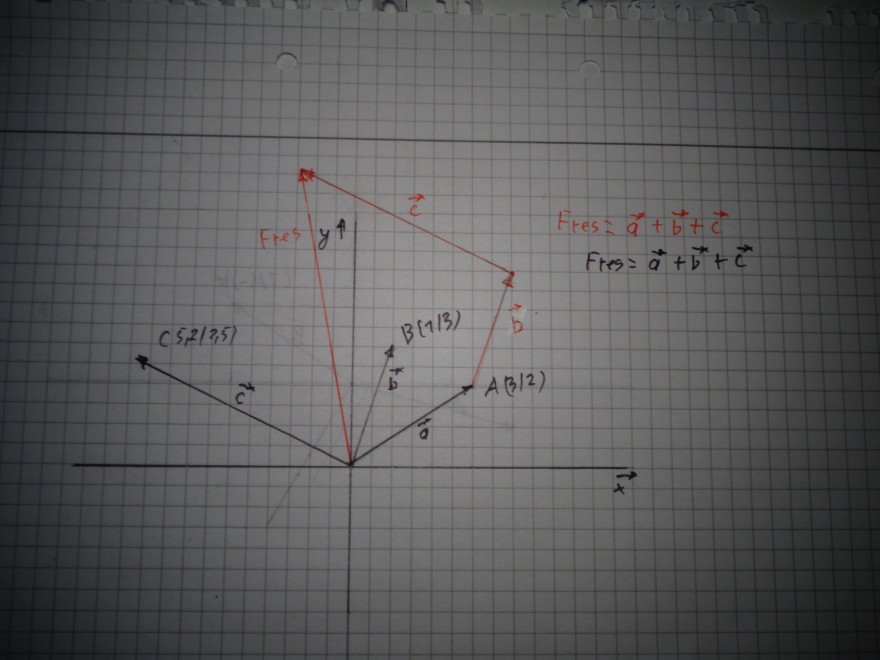
Vektoraddition

Text erkannt:

$=a^{*}+\vec{b}+c$
$m=\vec{a}+\vec{b}+\vec{c}$