a)
Die Dichtefunktion ist die Ableitung der Verteilungsfunktion.
b)
Die Quantilfunktion ist die Inverse der Verteilungsfunktion.
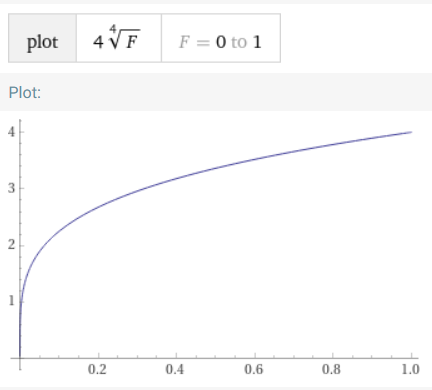
c)
Der Median ist dort, wo die Hälfte der Werte jeweils kleiner oder größer ist.
F(m) = 0,5
d)
Der Erwartungswert ist die Zahl, die die Zufallsvariable im Mittel annimmt.
E(X) = \( \int\limits_{-\infty}^{\infty} \) x f(x) dx
e)
Die Varianz ist die mittlere quadratische Abweichung der Zufallsvariablen von ihrem Erwartungswert.
V(X) = \( \int\limits_{-\infty}^{\infty} \) (x - E(X))2 f(x) dx
f)
\( \int\limits_{-\infty}^{12/5} \) f(x) = F(12/5) = ...