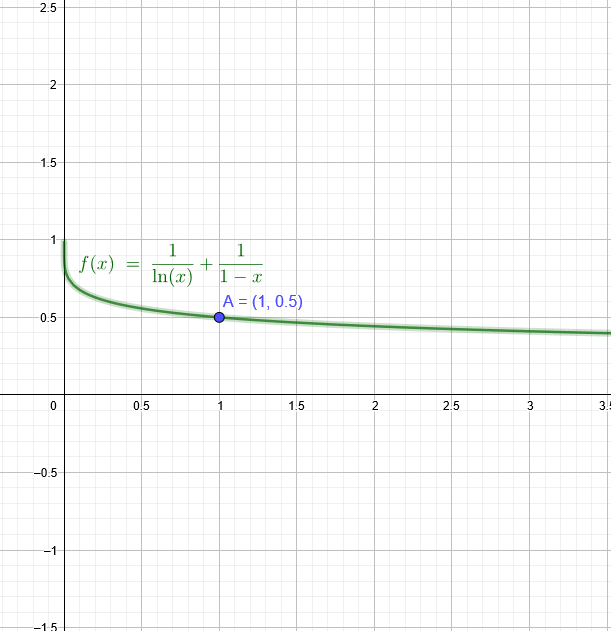
Ich stelle mal meinen Lösungsweg zum Vergleich ein:
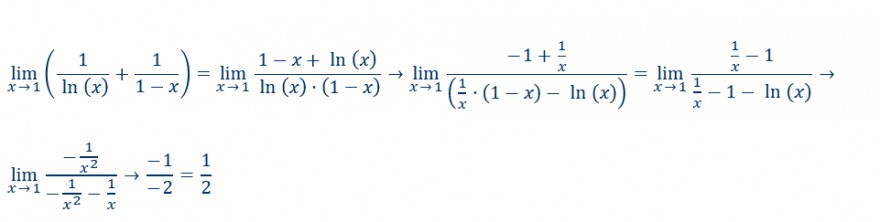
Text erkannt:
\( \lim \limits_{x \rightarrow 1}\left(\frac{1}{\ln (x)}+\frac{1}{1-x}\right)=\lim \limits_{x \rightarrow 1} \frac{1-x+\ln (x)}{\ln (x) \cdot(1-x)} \rightarrow \lim \limits_{x \rightarrow 1} \frac{-1+\frac{1}{x}}{\left(\frac{1}{x} \cdot(1-x)-\ln (x)\right)}=\lim \limits_{x \rightarrow 1} \frac{\frac{1}{x}-1}{\frac{1}{x}-1-\ln (x)} \rightarrow \)
\( \lim \limits_{x \rightarrow 1} \frac{-\frac{1}{x^{2}}}{-\frac{1}{x^{2}}-\frac{1}{x}} \rightarrow \frac{-1}{-2}=\frac{1}{2} \)