Dreieck: M halbiert die Strecke BC. Berechne die Länge der Strecke, den Winkel α und den Flächeninhalt des Dreiecks.

Question

Vom Dreieck \( \mathrm{ABC} \) sind gegeben:

\( \overline{\mathrm{AM}}=7,0 \mathrm{~cm} \)
\( \overline{\mathrm{BC}}=8,6 \mathrm{~cm} \)
\( \beta=46,2^{\circ} \)

M halbiert die Strecke \( \overline{B C} \). Berechne die Länge der Strecke \( \overline{\mathrm{AC}} \), den Winkel \( \alpha \) und den Flächeninhalt des Dreiecks.

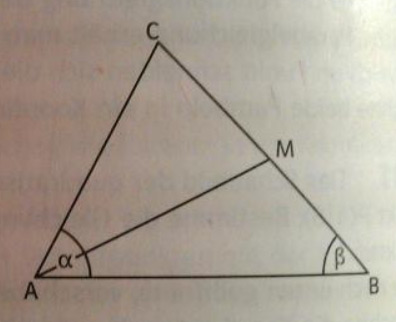
Ich soll es mit Trigometrie lösen (Cosinus, Sinus und Tangens).

Answer 1

Hi

sin β/AM = sin α'/(0.5 BM)
sin α' = (0.5 BM)/AM  sin β
-> α'

δ = 180° - α' - β
ε = 180° - δ

(AC)^2 = (AM)^2 + (CM)^2 - 2(AM)(CM) cos ε
-> AC

Reicht das als Ansatz?