Aloha :)
Ich schreibe \((x;y)\) anstatt \((x_1;x_2)\), das spart mir viele Indizes.$$f(x;y)=\frac{x^2+4y^2}{e^{4x^2+y^2}}=(x^2+4y^2)\cdot e^{-4x^2-y^2}$$
Mit der Produktregel bestimmen wir die partiellen Ableitungen:$$\partial_xf(x;y)=2xe^{-4x^2-y^2}+(x^2+4y^2)e^{-4x^2-y^2}(-8x)=-2e^{-4x^2-y^2}\left(4x^3+16xy^2-x\right)$$$$\partial_yf(x;y)=8ye^{-4x^2-y^2}+(x^2+4y^2)e^{-4x^2-y^2}(-2y)=-2e^{-4x^2-y^2}\left(x^2y+4y^3-4y\right)$$
An den stationären Punkten werden beide partiellen Ableitungen zugleich \(0\). Da die \(e\)-Funktion stets \(\ne0\) ist, müssen die Klammern verschwinden:$$0\stackrel!=4x^3+16xy^2-x=x\cdot(\,4(x^2+4y^2)-1\,)\implies x=0\;\lor\;(x^2+4y^2)=\frac14$$$$0\stackrel!=x^2y+4y^3-4y=y\cdot(\,(x^2+4y^2)-4\,)\;\;\;\;\implies y=0\;\lor\;(x^2+4y^2)=4$$
Das liefert 4 mögliche Kombinationen, die beide partiellen Ableitungen zu \(0\) machen können.
$$1)\quad x=0\;\land\;y=0$$$$2)\quad x=0\;\land\;(x^2+4y^2)=4\implies4y^2=4\implies y^2=1\implies y=\pm1$$$$3)\quad y=0\;\land\;(x^2+4y^2)=\frac14\implies x^2=\frac{1}{4}\implies x=\pm\frac12$$$$4)\quad(x^2+4y^2)=\frac14\;\land\;(x^2+4y^2)=4\;\leadsto\;\text{keine Lösung}$$
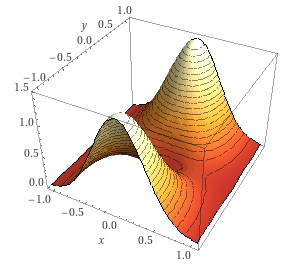
Die Funktion hat also fünf stationäre Punkte:$$P_1(0|0)\quad;\quad P_2\left(0|-1\right)\quad;\quad P_3\left(0|1\right)\quad;\quad P_4\left(-\frac12\bigg|0\right)\quad;\quad P_5\left(\frac12\bigg|0\right)$$
Zur Klassifizierung der stationären Punkte könnte man nun die Definitheit der Hesse-Matrix untersuchen, aber dafür werden mir die zweiten partiellen Ableitungen zu fummelig. Daher bestimmen wir zuerst die Funktionswerte an den stationären Punkten:$$f(0\;;\;0)=0\quad;\quad f(0\;;\;\pm1)=\frac4e\quad;\quad f\left(\pm\frac12\;;\;0\right)=\frac1{4e}$$
Da Quadratzahlen immer \(\ge0\) sind und die \(e\)-Funktion immer positiv ist, ist die Funktion stetes \(\ge0\). Mit zunehmendem Abstand vom Ursprung konvergiert sie gegen \(0\), weil der Nenner schneller wächst als der Zähler, erreicht den Wert \(0\) aber nie.
Daher ist der stationäre Punkt \(P_1(0|0)\) das globale Minimum.
Die beiden stationären Punkte \(P_2(0|-1)\) und \(P_3(0|+1)\) liefern von allen stationären Funktionswerten mit \(\frac4e\) den größten. Daher handelt es sich bei beiden Punkten um globale Maxima.
Die beiden stationären Punkte \(P_4(-\frac12|0)\) und \(P_5(\frac12|0)\) sind Sattelpunkte, weil die beiden globalen Extrema symmetrisch um sie herum herausragen.