Hallo Roland,
es gibt zwei Lösungen. Die triviale besteht darin, den Punkt \(B\) in den Punkt \(M\) zu schieben, wodurch dann eine Raute \(AMCD\) entsteht, die sich aus zwei gleichseitigen Dreiecken zusammen setzt.
Bei der zweiten Lösung heißt es: finde das Fünfeck! Dazu betrachte ich einen beliebigen Drachen mit den Ecken \(C\) und \(D\) auf dem Halbkreis und \(B\) auf \(AE\)
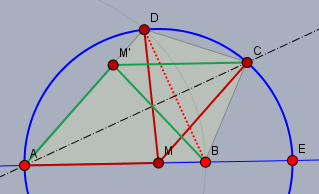
Die Strecken \(|MA|\), \(|MD|\) und \(|MC|\) (rot) haben alle die Länge \(r\). Da der Drache zu seiner Diagonalen \(AC\) symmetrisch ist, müssen auch die Strecken \(|M'A|\), \(|M'B|\) und \(M'C\) (grün) alle gleich lang und so lang wie \(r\) sein.
Weiter ist \(AMCM'\) eine Raute und somit immer \(M'C\) parallel zu \(AE\).
Wenn nun zusätzlich die Strecke \(|BD|=r\) sein soll ...
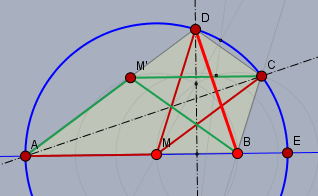
... so muss das Dreieck \(\triangle MBD\) ein gleichschenkliges sein und somit ist dessen Symmetrieachse (schwarz Strich-Punkt durch \(D\)) auch die Symmetrieachse des Fünfecks \(MBCDM'\), da alle Diagonalen gleich lang sind und wegen \(M'C \parallel MB\).
Und da die Seiten \(|BC|\) und \(|CD|\) ebenfalls gleich lang sind, muss es sich bei \(MBCDM'\) um ein regelmäßiges Fünfeck handeln! Also gilt$$\frac{|MC|}{|MB|} = \Phi \implies \frac{|MB|}{|BE|} = \Phi = \frac12(1+\sqrt 5)$$Gruß Werner