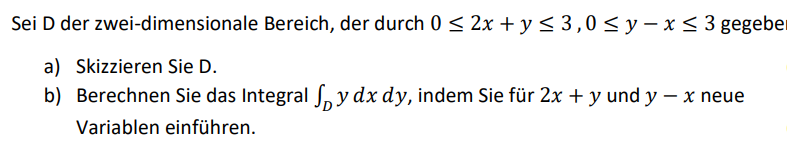
Text erkannt:
Sei \( \mathrm{D} \) der zwei-dimensionale Bereich, der durch \( 0 \leq 2 x+y \leq 3,0 \leq y-x \leq 3 \) gegebe
a) Skizzieren Sie D.
b) Berechnen Sie das Integral \( \int \limits_{D} y d x d y \), indem Sie für \( 2 x+y \) und \( y-x \) neue Variablen einführen.