Konvergenzkriterien bei Reihen

Question

Aufgabe:

Text erkannt:

Aufgabe 13 (Konvergenzkriterien für Reihen; $2+2+2+2$ Punkte). Entscheiden Sie, ob die folgenden Reihen konvergieren oder nicht.
a) $\sum \limits_{k=1}^{\infty} \frac{1}{\sqrt{k(k+1)}}$,
b) $\sum \limits_{k=1}^{\infty} \frac{5^{k / 2}}{k^{k}}$,
c) $\sum \limits_{k=1}^{\infty} \frac{k\left(2^{k}+1\right)}{3^{k}}$,
d) $\sum \limits_{k=1}^{\infty} \frac{k(k-1)}{\left(k^{2}+1\right)^{2}}$.

Dies ist meine Aufgabe

Problem/Ansatz:

Bei a) habe ich raus, das die Reihe divergiert

Text erkannt:

a) NB: $(a)_{k \in \mathbb{N}}$ ist eine Nullfolge
$a_{k}=\frac{1}{\sqrt{k(k+1)}}=\frac{1}{\sqrt{k^{2}+h}} \underset{k \rightarrow \infty}{\longrightarrow} 0$
HB
$\left|\frac{\sqrt{m(h+x)} \mid}{\sqrt{(m+x)(m+4)}}\right|=\frac{\sqrt{m} \cdot \sqrt{(h+1)}}{\sqrt{m+1} \sqrt{4-2}}=\frac{\sqrt{n}}{\sqrt{m+2}} \underset{k \rightarrow \infty}{\longrightarrow} 1$
Da es for $\frac{\sqrt{k}}{\sqrt{n+2}}$ hein 9 gibt, dass
$\frac{\sqrt{h}}{\sqrt{h+1}} \leq q<1$ ist, diver gieet die Reihe.

bei b), habe ich raus, dass die Reihe konvergiert

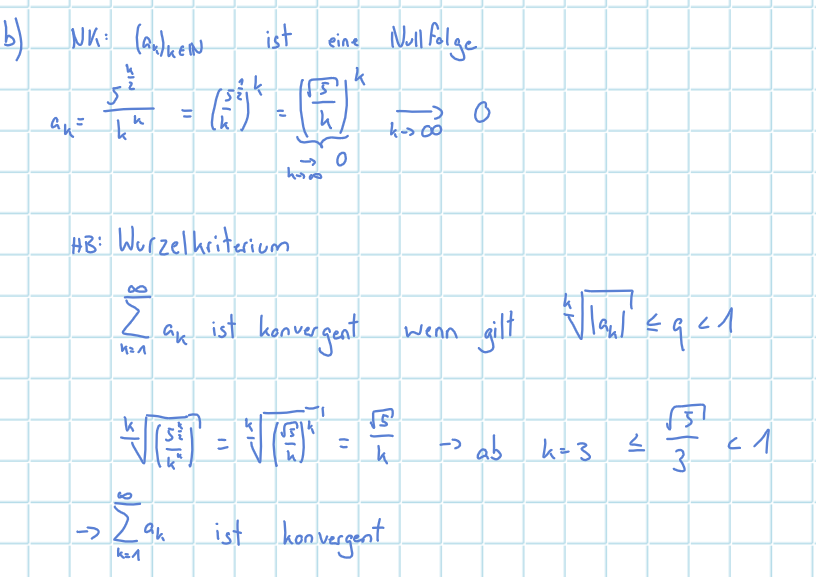
Text erkannt:

b) NK: $\left(a_{k}\right)_{k \in \mathbb{N}}$ ist eine Nollfolge
$a_{k}=\frac{5^{\frac{k}{2}}}{k^{k}}=\left(\frac{5_{k}}{k}\right)^{\frac{1}{2}}=\underbrace{\left(\frac{\sqrt{5}}{h}\right)^{k}}_{k \rightarrow \infty} \underset{k \rightarrow \infty}{\longrightarrow} 0$
HB: Wurzelhriterium
$\sum \limits_{k=1}^{\infty} a_{k}$ ist konvergent wenn gilt $\sqrt[k]{\left|a_{k}\right|} \leqslant q<1$
$\sqrt[k]{\left(\frac{5^{\frac{2}{2}}}{k^{4}}\right)}=\sqrt[k]{\left(\frac{\sqrt{3}}{k}\right)^{4}}=\frac{\sqrt{5}}{k} \rightarrow a b \quad k=3 \leq \frac{\sqrt{5}}{3}<1$
$\rightarrow \sum \limits_{k=1}^{\infty} a_{k}$ ist konvergent

bei c und d habe ich leider keinen Ansatz, könnte mir da jemand eine Hilfestellung geben. Außerdem wollte ich fragen, ob man die a und b so beweisen kann, wie ich das jetzt hier gemacht habe.

Vielen Dank schonmal im Voraus

Comments

Die Reihe aus (a) ist tatsächlich divergent. Die Begründung ist aber falsch.
Besser vielleicht: Die harmonische Reihe ist divergente Minorante.

---

Als Minorante müsste dann doch gelten, dass jeder Summand von ak größer als 1/k ist oder nicht? Das wäre hier ja nicht der Fall, könnte aber auch sein, dass ich das Kriterium flasch verstanden habe.

---

Prinzipiell hast du recht. Aus der Divergenz der Reihe $\sum\frac1k$ folgt aber unmittelbar auch die Divergenz der Reihen $\sum\frac1{2k}$ und $\sum\frac1{k+1}$. Tatsächlich gilt hier $a_k>\frac1{2k}$ und $a_k>\frac1{k+1}$.

---

Achso, ok vielen Dank

Answer 1

a) und b) finde ich gut .

c)  mit Quot.krit.

$\frac { \frac{(k+1)\left(2^{k+1}+1\right)}{3^{k+1}}} { \frac{k\left(2^{k}+1\right)}{3^{k}}}= \frac{(k+1)\left(2^{k+1}+1\right)3^{k}}{3^{k+1}k\left(2^{k}+1\right)} = \frac{(k+1)\left(2^{k+1}+1\right)}{3k\left(2^{k}+1\right)} = \frac{1}{3} \cdot \frac{(k+1)\left(2^{k+1}+1\right)}{k\left(2^{k}+1\right)}$

Der 2. Faktor geht gegen 2 also das ganze gegen 2/3 , ist also ab einem gewissen n kleiner als etwa 5/6 < 1,

also konvergent.

Comments

Vielen lieben Dank, das hat sehr weitergeholfen, hast du auch eine Idee, wie man an d rangehen kann?

---

a) ... finde ich gut .

Ich nicht.

---

Hatte da auch an Quot. krit. gedacht, krieg das aber nicht so recht hin.

Vielleicht kann man was abschätzen so in der Art

Die Summanden sind kleiner als 1/k² , also wäre die

Reihe mit 1/k² eine konvergente Majorante und diese

Reihe auch konvergent.

---

ok, vielen Dank nochmal, ich probier es dann mal mit dem abschätzen