Reißnagelwurf, wird 20 mal geworfen

Question

Aufgabe:

Reißnagelwurf
Ein Reißnagel wird 20-mal geworfen. Er bleibt im Mittel mit einer Wahrscheinlichkeit von
70% auf dem Kopf liegen.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass
a) der Reißnagel genau 14-mal in Kopflage kommt.
b) mehr als 10-mal die Kopflage einnimmt.
c) höchstens 10-mal in Seitenlage kommt.
d) zwischen 5- und 10-mal die Kopflage erreicht wird.
e) weniger als 5-mal Oder mehr als 15-mal die Kopllage eneicht wird.

Problem/Ansatz:

a) P(X=14)=(20 über 14) • 0,7^14 • 0,3^6

Bei den nächsten scheitere ich komplett

Answer 1

b) P(X>10) = P(X=11)+P(X=12)+...+P(X=20)

c) P(X<=10) = P(X=0)+P(X=1)+ ...+P(X=10) , p= 0,3

d) P(5<=X<=10) = P(X<=10) -P(X<=4)

e) P(X<5) +P(X>15) = P(X=0)+...+P(X=4) + P(X=16)+...+P(X=20)

Comments

Kann man das auch verkürzt aufschreiben oder ist die einzelne Rechnung, beispielsweise bei der b, notwendig?

Answer 2

Zur Hilfe und Selbstkontrolle kann man z.B. Geogebra verwenden.

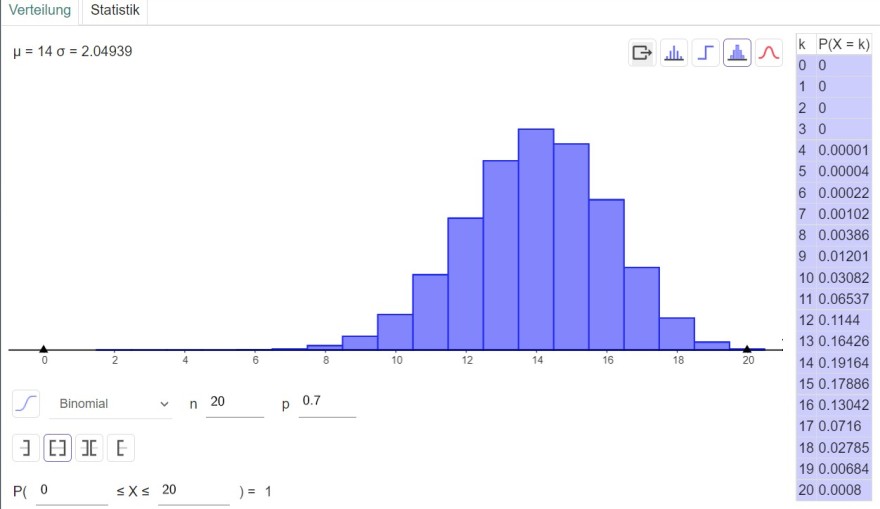
a) der Reißnagel genau 14-mal in Kopflage kommt.

P(X = 14) = ...

b) mehr als 10-mal die Kopflage einnimmt.

P(X > 10) = 1 - P(X ≤ 10) = ...

c) höchstens 10-mal in Seitenlage kommt.

P(X ≥ 10) = 1 - P(X ≤ 9) = ...

d) zwischen 5- und 10-mal die Kopflage erreicht wird.

Ich inkludiere die Grenzen 5 und 10 hier.

P(5 ≤ X ≤ 10) = P(X ≤ 10) - P(X ≤ 5) = ...

e) weniger als 5-mal Oder mehr als 15-mal die Kopllage eneicht wird.

P(X < 5) + P(X > 15) = 1 - P(5 ≤ X ≤ 15) = 1 - (P(X ≤ 15) - P(X ≤ 4)) = 1 - P(X ≤ 15) + P(X ≤ 4) = ...