Zunächst muss man sich klar machen, was der Grenzerlös überhaupt ist. Unter Erlös versteht man den Umsatz.
Der Erlös E ergibt sich aus Preis * Menge. Der Preis p ist in der Funktion p= 2560/x0,5 gegeben.
E = 2560/x^0,5 * x
Der Grenzerlös ist die Veränderung des Erlöses, wenn man die Menge um eine winzige Einheit erhöht. Das heißt, man muss ableiten.
Aber vorher vereinfachen wir die Formel noch etwas: die PAF kann man auch schreiben als 2650*x^-0,5 und der Erlös E sieht dann so aus: 2650*x^-0,5 * x ==> E = 2650*x^0,5
dE/dx = 0,5*2650 * x^-0,5
Im Cournotpunkt sind Grenzerlös und Grenzkosten (Ableitung der Kostenfunktion nach x) gleich.
Ein Beispiel findest du hier:
Auch Cournot Punkt genannt. Dieser Punkt gibt auf der Preis-Absatz-Funktion eines Monopolisten die Gewinnmaximale Menge und den Preis an. Ein Monopolist kann allein über den Preis entscheiden, zu dem er seine Produkte anbietet. Dabei muss er sich nicht an Wettbewerbern orientieren, sondern kann den Preis so setzen, dass er seinen Gewinn bzw. seinen Deckungsbeitrag maximiert. Die Berechnung wurde von Augustin Cournot gezeigt und daher ist dieser gewinnmaximale Punkt auch nach ihm benannt.
Die Abbildung zeigt den Verlauf der Erlöskurve, des Grenzerlöses, der Gewinnkurve, der Gesamtkosten und der Grenzkosten.
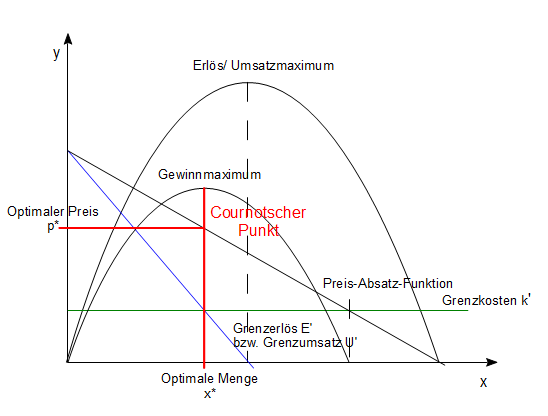
Berechnung des cournotschen Punktes
Zur Berechnung des cournotschen Punktes muss man die Preis-Absatzfunktion kennen.
x = x(p)
p = p(x): Der Preis p hängt von der verkauften Menge x ab.
U(x) = p(x)*x: Umsatz, Erlös
K(x): Gesamtkostenfunktion K(x) = kfix + kvar*x
Kfix: Fixkosten
Kvar: Variable Kosten
G(x) = U(x) – K(x)
Um das Gewinnmaximum zu berechnen, muss die erste Ableitung gebildet werden. Diese muss dann gleich null gesetzt werden
G‘(x) = U‘(x) – K‘(x) = 0
Daraus ergibt sich:
U‘(x) = K‘(x)
Die Grenzkosten K‘(x) sind im Gewinnmaximum genauso hoch wie der Grenzerlös.
Quelle: https://www.preissetzung.de/cournotscher-punkt/