ich weiß nicht, was Du mit "dem Py" meinst, aber vielleicht hilft Dir die Aufstellung der Funktionsgleichung:
Lineare Funktion allgemein:
y = mx + b
m ist die Steigung, diese berechnen wir, indem wir die "y-Differenz" durch die "x-Differenz" der beiden Punkte dividieren:
(-1-4)/(7-3) = -5/4
b ist der y-Achsenabschnitt; den erhalten wir, indem wir einen Punkt in die jetzt entstandene Gleichung
y = -5/4 * x + b
einsetzen, zum Beispiel P1(3;4)
4 = -5/4 * 3 + b
b = 4 + 15/4 = 31/4
Damit lautet die Funktionsgleichung
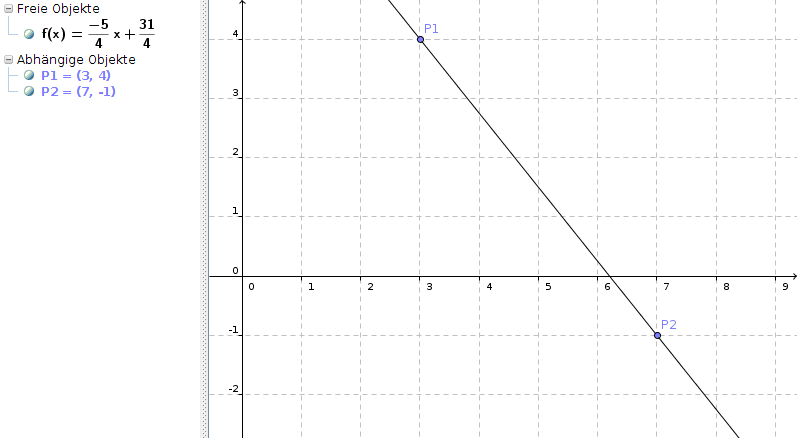
y = -5/4 * x + 31/4
Besten Gruß