Bestimmen Sie die Gerade gP, Q durch P und Q in \mathbb{P}2(\mathbb{F}3) .

Question

Gegeben seien die Punkte $P=[1: 1: 0]$ und $Q=[1: 2: 1]$ der projektiven Ebene $\mathbb{P}^{2}\left(\mathbb{F}_{3}\right)$. Bestimmen Sie die Gerade $g_{P, Q}$ durch $P$ und $Q$ in $\mathbb{P}^{2}\left(\mathbb{F}_{3}\right)$.

Comments

Wieso kann mir bei dieser Aufgabe niemand helfen?

---

Vielleicht, weil niemand versteht, was mit $P=[1: 1: 0]$ und $Q=[1: 2: 1]$ gemeint ist. Welche Bedeutung hat hier der Doppelpunkt :?

---

das sind homogene Koordinate und $P$ liegt im unendlichen .. .habe jetzt aber keine Zeit.

Das Ergebnis ist $g_{PQ}=[1:-1:1]$

---

hier ist das ergebnis: Aber ich bräuchte eine erklärung.

BeweIs: Es gilt wegen $[1: 1: 0] \in g_{P, Q}$ und $[1: 2: 1] \in g_{P, Q}$, dass $a+b=0$ und $a+2 b+c=0$ ist. Letzteres können wir auch als $a+b+b+c=0$ aufschreiben und es folgt wegen der ersten Gleichung, dass $b+c=0$ und somit $a=c$ ist. Im $\mathbb{F}_{3}$ haben wir bekanntlich nur die Elemente 0 , 1 und 2. Diese probieren wir nacheinander für $a$ aus und schauen, was passiert (alternativ kann man auch ganz normal die Gleichung lösen). Im Fall $a=0$ wären wegen der Additionstabelle von $\mathbb{F}_{3}$ auch $b=0$ und $c=0$, was gegen die Voraussetzung von Definition 6.2.3. verstößt. Eine Gerade mit $a=0$ kann es folglich nicht geben. Im Fall $a=c=1$ wäre $b=2$ und im Fall $a=c=2$ wäre

$b=1$. Diese beiden Möglichkeiten sind dementsprechend die einzigen Möglichkeiten, sodass $g_{P, Q}=\left\{[x: y: z] \in \mathbb{P}^{2}\left(\mathbb{F}_{3}\right) \mid x+2 y+z=0\right\}$ und $g_{P, Q}^{\prime}=\left\{[x: y: z] \in \mathbb{P}^{2}\left(\mathbb{F}_{3}\right) \mid 2 x+y+2 z=0\right\}$ die einzigen möglichen Geraden sind. Es sollte jedoch nur genau eine Gerade durch $P$ und $Q$ geben. Tatsächlich ist auch $g_{P, Q}=g_{P, Q}^{\prime}$, denn in $\mathbb{F}_{3}$ gilt
$x+2 y+z=0 \Longleftrightarrow-(x+2 y+z)=0 \quad \Longleftrightarrow \quad-x-2 y-z=2 x+y+2 z=0 .$

---

Hallo

du hast doch die Erklärungen gut aufgeschrieben, was fehlt dabei?

lul

---

Ich versteh das trotzdem nicht.

---

Ich versteh das trotzdem nicht.

Ich habe Dir den Versuch einer Erklärung als Antwort (s.u.) geschrieben. Frage bitte nach, falls irgendetwas unklar ist.

Answer 1

Hallo,

hier ist das Ergebnis: Aber ich bräuchte eine Erklärung.

Nehmen wir mal kurz an, die projektive Ebene wäre über dem Körper $\mathbb{R}$ definiert - also $P,Q\in \mathbb{P}^2(\mathbb{R})$. Dann sähe das im Bild so aus:

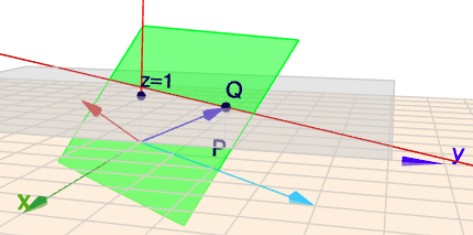
Die projektive Ebene ist die Ebene parallel zur XY-Ebene bei $z=1$. Jeder Punkt der Ebene ist gegeben durch den Schnittpunkt einer Ursprungsgerade mit eben dieser Ebene. Für den Punkt $Q$ habe ich den (blauen) Vektor der Ursprungsgeraden eingezeichnet und den Schnittpunkt $Q$ gekennzeichnet. Die Ursprungsgerade von $P$ (hellblauer Pfeil) verläuft parallel (bzw. in) zur XY-Ebene und es gibt keinen Schnittpunkt. Daher liegt der Punkt $P$ im unendlichen.

Das bedeutet aber auch, dass jede Gerade 'durch' $P$ parallel zur Ursprungsgerade von $P$ verlaufen muss. Also ist die gesuchte Gerade die Gerade durch $Q$, die parallel zur Ursprungsgerade von $P$ verläuft. Ich habe diese Gerade rot eingezeichnet. Klicke auf das Bild, dann öffnet sich Geoknecht3D, und Du kannst die Szene rotieren für einen besseren dreidimensionalen Eindruck.

Sowie jeder Punkt durch seine Ursprungsgerade gegeben ist, so ist jede Gerade durch eine Ursprungsebene gegeben. Der roten Geraden kann eindeutig die grüne Ursprungsebene zugeordnet werden. Und natürlich müssen beide Ursprungsgeraden (die von $P$ und $Q$) innerhalb dieser Ebene liegen. Da der Normalenvektor $n_{g(P,Q)}$ (rot) dieser Ebene auf beiden Ursprungsgeraden von $P$ und $Q$ senkrecht steht, ist dieser schlicht das Kreuzprodukt der beiden 'Punkte':$$n_{g(P,Q)} = P\times Q = \begin{pmatrix}1\\ 1\\ 0\end{pmatrix}\times \begin{pmatrix}1\\ 2\\ 1\end{pmatrix} = \begin{pmatrix}1\\ -1\\ 1\end{pmatrix}$$Da wir uns aber im $\mathbb{P}(\mathbb{F}_3)$ befinden und $$-1\equiv 2 \mod 3$$ist, ist der Normalenvektor $n_{g(P,Q)}$ und somit die Gerade $g_{P,Q}$:$$n_{g(P,Q)}\begin{pmatrix}1\\ 2\\ 1\end{pmatrix} \implies g_{P,Q}:\space x+2z+1=0$$

Der Lösungsweg, der in Deiner Lösung beschritten wurde, sieht so aus:

Eine Gerade der projektiven Ebene hat allgemein die Form$$g:\quad ax+by+cz = 0$$und die Parameter a, b und c müssen so gewählt werden, dass die Punkte $P$ und $Q$ dort enthalten sind. Einsetzen liefert:$$\begin{aligned} a\cdot 1 + b\cdot 1 + c \cdot 0&= 0 \\ a \cdot 1 + b \cdot 2 + c \cdot 1 &= 0\end{aligned}$$Oben steht $a+b=0$. Zieht man die erste von der zweiten ab, bleibt $b+c=0$. Man kann nun getrost $c=1$ setzen, worauf dann sofort $a=1$ und $b=-1\equiv 2$ folgt, also das bekannte Ergebnis. Bei der oben beschriebenen Lösung hat man es sich noch zunutze gemacht, dass es für jeden Parameter nur drei  Möglichkeiten gibt: $\{0,1,2\} = \mathbb{F}_3$. Wegen $a+b=0$ scheidet $a=0$ sofort aus (warum?). Beibt $a=1$ und $a=2$, was aber in beiden Fällen zur identischen Lösung führt. Multipliziere die zweite Lösung $2x+y+2z=0$ mit $2$ (in $\mathbb{F}_3$) und Du erhältst die erste Lösung. Hinweis$$2\cdot 2 \equiv 1 \mod 3$$

Gruß Werner