Winkel berechnen und allgemein darstellen

Question

Aufgabe:

Winkel berechnen und allgemein Darstellen

Problem/Ansatz:

Irgendwie habe ich 2 unbekannte in meiner Gleichung…

Answer 1

Verstehst du, warum in der oberen Abbildung diese drei Winkel die Größen φ+36°, φ+36° und 108°- 2φ haben?

Daraus ergeben sich die in der zweiten Abbildung grün und rot angegebenen Winkelgrößen. Du musst nur noch die rote Gleichung nach φ auflösen. (Ich erhalte 12°.)

Comments

Kommst du auf die 36 wegen den Stufen-/Wechselwinkel?

---

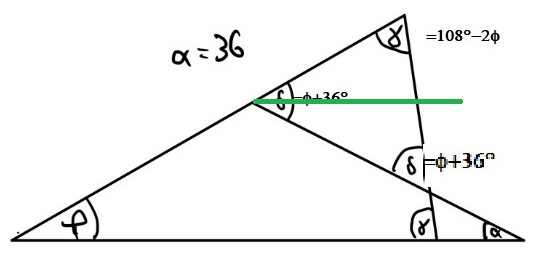
Kommst du auf die 36 wegen den Stufen-/Wechselwinkel?

Siehst du hier parallele Geraden???

Die 36 (Grad) verwende ich, weil alpha so gegeben ist.

Kennst du den Außenwinkelsatz?

PS: Man kann tatsächlich nach Einzeichnen einer Hilfslinie (grün) der Stufen- und Wechselwinkelsatz anwenden. Man hat oberhalb phi und unterhalb alpha=36°.

---

Jetzt hats geklickt. Danke für die Hilfe

Answer 2

Ich sehe 3 Dreiecke und in jedem gilt die Innenwinkelsumme von 180 Grad.

2·γ + φ = 180
2·δ + γ = 180
φ + 180 - δ + 36 = 180 --> γ = 84 ∧ δ = 48 ∧ φ = 12

Answer 3

\(\varphi+\alpha+(180^\circ - \delta)=180^\circ\Rightarrow \varphi+\alpha=\delta\\2\delta+\gamma=180^\circ\Rightarrow\gamma=180^\circ-2\varphi-2\alpha\\ \varphi+2\gamma=180^\circ\Rightarrow \varphi+2(180^\circ-2\varphi-2\alpha)=180^\circ\\ \Rightarrow 180^\circ-4\alpha=3\varphi\\ \Rightarrow \varphi = 60^\circ- \frac43\alpha        \)